题目内容
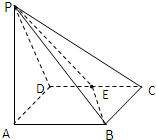 如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°
如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°(1)求证:平面EPB⊥平面PBA;
(2)求二面角B-PD-A的平面角正切值的大小.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间角
分析:(1)由已知条件推导出BE⊥AB,PA⊥BE,由此能证明BE⊥面PAB,从而得到面PBE⊥平面PAB.
(2)过B点作BF⊥AD于F,过F作FM⊥PD于M,连结BM,由已知条件推导出∠BMF为二面角B-PD-A的平面角,由此能求出二面角B-PD-A平面角正切值.
(2)过B点作BF⊥AD于F,过F作FM⊥PD于M,连结BM,由已知条件推导出∠BMF为二面角B-PD-A的平面角,由此能求出二面角B-PD-A平面角正切值.
解答:
解:(1)∵E为CD的中点,BC=1,ABCD为菱形,
∴CE=
,又∠BCD=60°,∴∠BEC=90°,
∴BE⊥AB,又PA⊥平面ABCD,
∴PA⊥BE,PA?面PAB,AB?面PAB,PA∩AB=A,
∵BE⊥面PAB,∵BE?平面PBE,
∴面PBE⊥平面PAB.(4分)
(2)过B点作BF⊥AD于F,过F作FM⊥PD于M,连结BM,
∵BF⊥AD,BF⊥PA,∴BF⊥面PAD,
∵BM为面PAD的斜线,MF为BM在面PAD的射影,∴BM⊥PD,
∴∠BMF为二面角B-PD-A的平面角,(8分)
PC与面ABCD成角60°,∠PCA=60°,PA=3,
BF=
,MF=
,∠BMF=
,
∴二面角B-PD-A平面角正切值为
.(12分)
∴CE=
| 1 |
| 2 |
∴BE⊥AB,又PA⊥平面ABCD,
∴PA⊥BE,PA?面PAB,AB?面PAB,PA∩AB=A,
∵BE⊥面PAB,∵BE?平面PBE,
∴面PBE⊥平面PAB.(4分)
(2)过B点作BF⊥AD于F,过F作FM⊥PD于M,连结BM,
∵BF⊥AD,BF⊥PA,∴BF⊥面PAD,
∵BM为面PAD的斜线,MF为BM在面PAD的射影,∴BM⊥PD,
∴∠BMF为二面角B-PD-A的平面角,(8分)
PC与面ABCD成角60°,∠PCA=60°,PA=3,
BF=
| ||
| 2 |
| 3 | ||
2
|
| ||
| 3 |
∴二面角B-PD-A平面角正切值为
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
复数z=1+i(i为虚数单位),
为z的共轭复数,则下列结论正确的是( )
. |
| z |
A、
| ||||
B、
| ||||
C、z•
| ||||
D、
|
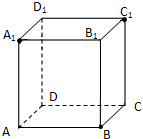 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.