题目内容

设y=sin2x，则y′=（　　）
A、sin2x
B、2sinx
C、cos2x
D、cos2x
考点：导数的运算
专题：导数的概念及应用
分析：直接利用简单的复合函数的求导运算进行计算．
解答： 解：因为y=sin2x，
所以y′=2sinxcosx=sin2x．
故选：A．
点评：本题考查了简单的复合函数的导数，解答此题的关键是不要忘记对内层函数进行求导，是基础题．
练习册系列答案
相关题目
对于集合A={a1，a2，…，an}（n∈N*，n≥3），定义集合S={x|x=ai+aj，1≤i＜j≤n}，记集合S中的元素个数为S（A）．若a1，a2，…，an是公差大于零的等差数列，则S（A）=
 
．
已知
b+i
a+2i
=1+i（a，b∈R），其中i为虚数单位，则a+b=
 
．
已知等比数列{an}满足a1+a2=4，a2+a3=8，则a5=
 
．
给出如下四个判断：
①?x0∈R，ex0≤0；
②?x∈R+，2x＞x2；
③设集合A={x|
x-1
x+1
＜0}，B={x|x-1|＜a}，则“a=1”是“A∩B≠∅”的必要不充分条件；  
④
a
，
b
为单位向量，其夹角为θ，若|
a
-
b
|＞1，则
π
3
＜θ≤π．
其中正确的判断个数是（　　）
A、1B、2C、3D、4
等比数列{an}中，a2=1，a8=64，则a5=（　　）
A、8B、12
C、8或-8D、12或-12
复数z=1+i（i为虚数单位），
.
z
为z的共轭复数，则下列结论正确的是（　　）
A、
.
z
的实部为-1
B、
.
z
的虚部为1
C、z•
.
z
=2
D、
.
z
z
=i
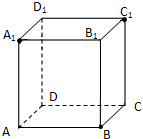已知正方体ABCD-A1B1C1D1．
（1）求异面直线BA1和CC1的夹角是多少？
（2）求A1B和平面CDA1B1所成的角？
（3）求平面CDA1B1和平面ABCD所成二面角的大小？
小昆和小鹏两人站成一列，背着墙，面朝太阳，小昆靠近墙，在太阳光照射下，小昆的头部影子正好落在墙角处．如果小昆身高为1.6m，离墙距离为3m，小鹏的身高1.5m，离墙的距离为5m，则小鹏的身影是否在小昆的脚下，请通过计算说明
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网