题目内容
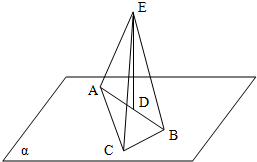如图，已知Rt△ABC在平面α内，D是斜边AB的中点，DE⊥α，且DE=12cm，AC=8cm，BC=6cm，求EA、EB、EC的长．考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：连接CD，利用勾股定理先求得AB，进而可知AD，BD，CD的长度，最后利用勾股定理分别求得EA、EB、EC．
解答：
解：连接CD，
AB=
=10，
∴AD=DB=5，CD=
AB=5
∵DE⊥α，
∴DE⊥AB，DE⊥CD，
∴AE=BE=
=
=13，
CD=
=13．
AB=
| 64+36 |
∴AD=DB=5，CD=
| 1 |
| 2 |
∵DE⊥α，
∴DE⊥AB，DE⊥CD，
∴AE=BE=
| AD2+DE2 |
| 25+144 |
CD=
| CD2+DE2 |
点评：本题主要考查了线面垂直的性质，勾股定理在解三角形中的应用．考查了学生对基础知识的灵活运用．
练习册系列答案
相关题目
若点P在曲线y=x3-x上移动，则过P点的切线的倾斜角的取值范围是（ ）
| A、[0，π） | ||||||
B、（0，
| ||||||
C、[0，
| ||||||
D、[0，
|
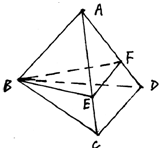已知正三棱锥A-BCD中，底面边长为a，侧棱长为2a，过B点作与则棱AC、AD相交的截面BEF，在这个截面三角形中，求：
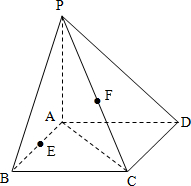已知PA⊥平面ABCD，四边形ABCD为正方形，PA=AB=4，E、F分别为AB、PC的中点．
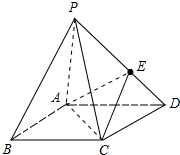如图，底面是平行四边形的四棱锥P-ABCD，点E在PD上，且PE：ED=2：1，问：在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论．