题目内容
已知f(x)是定义在R上的偶函数,当x≥0时,f(x)单调递减,设f(1-m)<f(m),求m的取值范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据f(x)是偶函数,结合当x≥0时,f(x)单调递减,可以大体画出该函数图象草图,可以发现,该函数图象关于y轴对称,且离对称轴越近的点,纵坐标越大,依此可构造关于m的不等式.
解答:
解:∵f(x)是定义在R上的偶函数,当x≥0时,f(x)单调递减,
∴可画出该函数的草图如下:
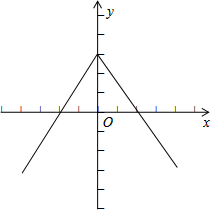
可见,该函数图象关于y轴对称,且离对称轴越近的点,函数值越大,
∵设f(1-m)<f(m),∴|1-m|>|m|,
∴(1-m)2>m2,解得m<
.
∴可画出该函数的草图如下:
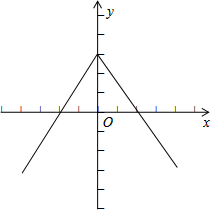
可见,该函数图象关于y轴对称,且离对称轴越近的点,函数值越大,
∵设f(1-m)<f(m),∴|1-m|>|m|,
∴(1-m)2>m2,解得m<
| 1 |
| 2 |
点评:这是一道考查抽象函数的性质的问题,一般采用数形结合的方法来解.本题还要注意绝对值不等式的转化方法及变形依据.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
若不等式x2-logax≤0在x∈(0,
]内恒成立,则a的取值范围是( )
| 1 |
| 2 |
A、0<a≤
| ||
B、0<a<
| ||
C、
| ||
D、
|
 有一个正三棱柱锤A-BCD零件,P是侧面ACD上一点,在面ACD上过点P画一条与棱AB垂直的线段,怎样画法?并说明理由.
有一个正三棱柱锤A-BCD零件,P是侧面ACD上一点,在面ACD上过点P画一条与棱AB垂直的线段,怎样画法?并说明理由.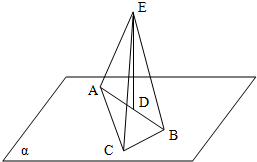 如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.
如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.