题目内容
已知函数f(x)=cos(2x+
),x∈R.
(1)求f(-
)的值;
(2)设α是第二象限角,sinα=
,求f(α+
)的值.
| π |
| 6 |
(1)求f(-
| π |
| 2 |
(2)设α是第二象限角,sinα=
| 1 |
| 3 |
| π |
| 6 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:(1)将x=-
代入f(x)=cos(2x+
)计算即可;
(2)依题意,利用同角三角函数间的关系可求得cosα,从而可求得f(α+
)的值.
| π |
| 2 |
| π |
| 6 |
(2)依题意,利用同角三角函数间的关系可求得cosα,从而可求得f(α+
| π |
| 6 |
解答:
(1)f(-
)=cos(-π+
)=-cos
=-
…(5分)(第二个等号(3分),其他各1分)
(2)f(α+
)=cos(2α+
)=-sin2α=-2sinαcosα…(9分)(第三个等号(2分),其他各1分)
sinα=
,α是第二象限角,cosα=-
=-
…(12分)(第一个等号2分)
所以f(α+
)=cos[2(α+
)+
]=-sin2α=-2sinαcosα=-2×
×(-
)=
…(14分)
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
(2)f(α+
| π |
| 6 |
| π |
| 2 |
sinα=
| 1 |
| 3 |
| 1-sin2α |
2
| ||
| 3 |
所以f(α+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 3 |
2
| ||
| 3 |
4
| ||
| 9 |
点评:本题考查同角三角函数间的关系与两角和与差的余弦函数,考查运算求解能力,属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
两条异面直线指的是( )
| A、没有公共点的两条直线 |
| B、分别位于两个不同平面的两条直线 |
| C、某一平面内的一条直线和这个平面外的一条直线 |
| D、不同在任何一个平面内的两条直线 |
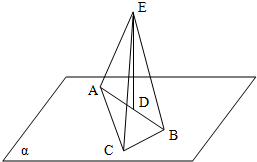 如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.
如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长. 如图,长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a.
如图,长方体ABCD-A1B1C1D1中,AB=BC=a,AA1=2a.