题目内容
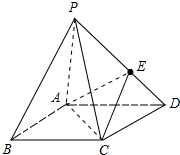如图，底面是平行四边形的四棱锥P-ABCD，点E在PD上，且PE：ED=2：1，问：在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：取棱PC的中点F，线段PE的中点M，连接BD．设BD∩AC=O．连接BF，MF，BM，OE．结合菱形的性质及三角形中位线定理及面面平行的判定定理可得平面BMF∥平面AEC，进而由面面平行的性质得到BF∥平面AEC．
解答：
解：存在点F为PC的中点，使BF∥平面AEC
理由如下：
取棱PC的中点F，线段PE的中点M，连接BD．设BD∩AC=O．
连接BF，MF，BM，OE．
∵PE：ED=2：1，F为PC的中点，E是MD的中点，
∴MF∥EC，BM∥OE．
∵MF?平面AEC，CE?平面AEC，BM?平面AEC，OE?平面AEC，
∴MF∥平面AEC，BM∥平面AEC．
∵MF∩BM=M，
∴平面BMF∥平面AEC．
又BF?平面BMF，
∴BF∥平面AEC．
解：存在点F为PC的中点，使BF∥平面AEC理由如下：
取棱PC的中点F，线段PE的中点M，连接BD．设BD∩AC=O．
连接BF，MF，BM，OE．
∵PE：ED=2：1，F为PC的中点，E是MD的中点，
∴MF∥EC，BM∥OE．
∵MF?平面AEC，CE?平面AEC，BM?平面AEC，OE?平面AEC，
∴MF∥平面AEC，BM∥平面AEC．
∵MF∩BM=M，
∴平面BMF∥平面AEC．
又BF?平面BMF，
∴BF∥平面AEC．
点评：题考查的知识点是直线与平面平行的判定，关键是证得平面BMF∥平面AEC．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
| ∫ | 1 0 |
| 1-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
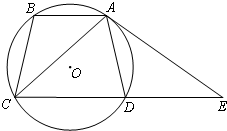如图，等腰梯形ABCD内接于⊙O，AB∥CD．过点A作⊙O的切线交CD的延长线于点E．求证：∠DAE=∠BAC．
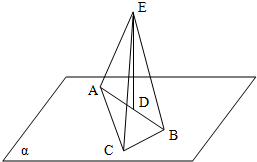如图，已知Rt△ABC在平面α内，D是斜边AB的中点，DE⊥α，且DE=12cm，AC=8cm，BC=6cm，求EA、EB、EC的长．
如图，长方体ABCD-A1B1C1D1中，AB=BC=a，AA1=2a．