题目内容
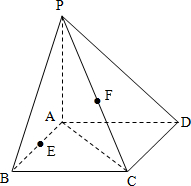 已知PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,E、F分别为AB、PC的中点.
已知PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,E、F分别为AB、PC的中点.(1)求PC与平面PAB所成角的大小;
(2)求异面直线PE与AC所成角的大小;
(3)求二面角A-PB-C的大小.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)由BC⊥AB,BC⊥PA,知PC与平面PAB所成的角为∠PCB,由此能求出PC与平面PAB所成角的大小.
(2)连结AC,过E作EG∥AC,交BC于G,则∠PGC就是异面直线PE与AC所成角,由此能求出异面直线PE与AC所成角为45°.
(3)取PB的中点点H,连结AH,HF,AF,则二面角A-PB-C的平面角为∠AHF,由此能求出二面角A-PB-C的大小.
(2)连结AC,过E作EG∥AC,交BC于G,则∠PGC就是异面直线PE与AC所成角,由此能求出异面直线PE与AC所成角为45°.
(3)取PB的中点点H,连结AH,HF,AF,则二面角A-PB-C的平面角为∠AHF,由此能求出二面角A-PB-C的大小.
解答:
解:(1)∵BC⊥AB,BC⊥PA,
∴PC与平面PAB所成的角为∠PCB,
∵PA=AB=4,∴PB=4
,
∵BC=4,∴PC=4
,
∴sin∠PCB=
,∴∠PCB=arcsin
.
∴PC与平面PAB所成角的大小为arcsin
.
(2)连结AC,过E作EG∥AC,交BC于G,
则∠PGC就是异面直线PE与AC所成角,
∵PE=
=2
,EG=
=2
,
PG=
=6,
∴cos∠PGC=
=
,∴∠PGC=45°.
∴异面直线PE与AC所成角为45°.
(3)取PB的中点点H,连结AH,HF,AF,
∵AH⊥PB,HF⊥PB,
∴二面角A-PB-C的平面角为AHF,
∵AH=
=2
,HF=
=2,AF=
=2
,
cos∠AHF=
=0,∴∠AHF=90°.
∴二面角A-PB-C的大小为90°.
∴PC与平面PAB所成的角为∠PCB,

∵PA=AB=4,∴PB=4
| 2 |
∵BC=4,∴PC=4
| 3 |
∴sin∠PCB=
| ||
| 3 |
| ||
| 3 |
∴PC与平面PAB所成角的大小为arcsin
| ||
| 3 |
(2)连结AC,过E作EG∥AC,交BC于G,
则∠PGC就是异面直线PE与AC所成角,
∵PE=
| 42+22 |
| 5 |
4
| ||
| 2 |
| 2 |
PG=
| 42+42+22 |
∴cos∠PGC=
| 36+8-20 | ||
2•6•2
|
| ||
| 2 |
∴异面直线PE与AC所成角为45°.
(3)取PB的中点点H,连结AH,HF,AF,
∵AH⊥PB,HF⊥PB,
∴二面角A-PB-C的平面角为AHF,
∵AH=
4
| ||
| 2 |
| 2 |
| 4 |
| 2 |
4
| ||
| 2 |
| 3 |
cos∠AHF=
| 8+4-12 | ||
2•2
|
∴二面角A-PB-C的大小为90°.
点评:本题考查直线与平面所成角的大小的求法,考查异面直线所成角的大小的求法,考查二面角的大小的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
已知函数f(x)=
,满足?x1≠x2,都有
<0成立,则a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
| A、(0,1) | ||
| B、(1,+∞) | ||
C、(0,
| ||
D、(0,
|
下列一定在一个平面内的图形是( )
| A、垂直于同一直线的两条直线 |
| B、顺次首尾相连的四条线段 |
| C、两两相交的三条直线 |
| D、分别在两条异面直线上两点连线的中点的轨迹 |
 有一个正三棱柱锤A-BCD零件,P是侧面ACD上一点,在面ACD上过点P画一条与棱AB垂直的线段,怎样画法?并说明理由.
有一个正三棱柱锤A-BCD零件,P是侧面ACD上一点,在面ACD上过点P画一条与棱AB垂直的线段,怎样画法?并说明理由.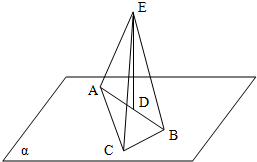 如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.
如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.