题目内容
设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作.若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元.
(Ⅰ)设X表示一周5天内机器发生故障的天数,求X的分布列;
(Ⅱ)以Y表示一周内所获利润,则一周内利润的期望是多少?
(Ⅰ)设X表示一周5天内机器发生故障的天数,求X的分布列;
(Ⅱ)以Y表示一周内所获利润,则一周内利润的期望是多少?
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)以X表示一周5天内机器发生故障的天数,则X-B(5,0.2),由此能求出X的分布列.
(Ⅱ)以Y表示一周内所获利润,则y=g(X)=
,一周内利润的期望值.
(Ⅱ)以Y表示一周内所获利润,则y=g(X)=
|
解答:
解:(Ⅰ)以X表示一周5天内机器发生故障的天数,则X-B(5,0.2),
P(X=k)=
0.2k0.85-k,k=0,1,2,3,4,5,
∴X的分布列为:
(Ⅱ)以Y表示一周内所获利润,
则y=g(X)=
,
P(Y=10)=P(X=0)=0.32768,
P(Y=5)=P(X=1)=0.4096,
P(Y=0)=P(X=2)=0.2048,
P(Y=-2)=P(X≥3)=0.0512+0.0064+0.00032=0.05792,
∴一周内利润的期望为:
EY=10×0.32768+5×0.4096+(-2)×0.05792=5.20896(万元).
P(X=k)=
| C | k 5 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| p | 0.32768 | 0.4096 | 0.2048 | 0.0512 | 0.0064 | 0.00032 |
则y=g(X)=
|
P(Y=10)=P(X=0)=0.32768,
P(Y=5)=P(X=1)=0.4096,
P(Y=0)=P(X=2)=0.2048,
P(Y=-2)=P(X≥3)=0.0512+0.0064+0.00032=0.05792,
∴一周内利润的期望为:
EY=10×0.32768+5×0.4096+(-2)×0.05792=5.20896(万元).
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
下列一定在一个平面内的图形是( )
| A、垂直于同一直线的两条直线 |
| B、顺次首尾相连的四条线段 |
| C、两两相交的三条直线 |
| D、分别在两条异面直线上两点连线的中点的轨迹 |
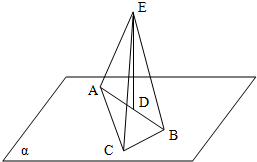 如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.
如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.