题目内容
（文科）设函数f（x）=
是奇函数，则实数a的值为 ．
| ex+ae-x |
| x2 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：利用奇函数的定义f（-x）=-f（x）恒成立，列出关于a的方程求解．
解答：
解：函数f（x）=
是奇函数，
∴f（-x）=f（x），即
=-
恒成立，
即
=
恒成立，
∴a=-1．
故答案为：-1．
| ex+ae-x |
| x2 |
∴f（-x）=f（x），即
| e-x+aex |
| (-x)2 |
| ex+ae-x |
| x2 |
即
| aex+e-x |
| x2 |
| -ex-ae-x |
| x2 |
∴a=-1．
故答案为：-1．
点评：在定义域关于原点对称的前提下，函数的奇偶性实际上是f（-x）=-f（x）与f（-x）=f（x）两个恒等式的问题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
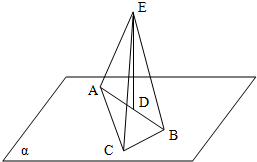如图，已知Rt△ABC在平面α内，D是斜边AB的中点，DE⊥α，且DE=12cm，AC=8cm，BC=6cm，求EA、EB、EC的长．