题目内容
若点P在曲线y=x3-x上移动，则过P点的切线的倾斜角的取值范围是（ ）
| A、[0，π） | ||||||
B、（0，
| ||||||
C、[0，
| ||||||
D、[0，
|
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求函数的导数，利用导数的几何意义，结合正切函数的图象和性质即可得到结论．
解答：
解：∵y=x3-x，
∴y′=3x2-1≥-1，
∴tanα≥-1，
过P点的切线的倾斜角的取值范围是α∈[0，
）∪[
，π），
故选：D．
∴y′=3x2-1≥-1，
∴tanα≥-1，
过P点的切线的倾斜角的取值范围是α∈[0，
| π |
| 2 |
| 3π |
| 4 |
故选：D．
点评：本题主要考查导数的几何意义以及正切函数的图象和性质，综合性较强．
练习册系列答案
相关题目
数列
，
，
，
，…的一个通项公式为（ ）
| 1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 15 |
| 1 |
| 24 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
下列推理是归纳推理的是（ ）
| A、A，B为定点，动点P满足|PA|+|PB|=2a＞|AB|，得P的轨迹为椭圆 | ||||
| B、科学家利用鱼的沉浮原理制造潜艇 | ||||
C、由圆x2+y2=r2的面积πr2，猜出椭圆
| ||||
| D、由a1=1，an=3n-1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式 |
已知函数f（x）=
，满足?x1≠x2，都有
＜0成立，则a的取值范围是（ ）
|
| f(x1)-f(x2) |
| x1-x2 |
| A、（0，1） | ||
| B、（1，+∞） | ||
C、（0，
| ||
D、（0，
|
| ∫ | 1 0 |
| 1-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
若不等式x2-logax≤0在x∈（0，
]内恒成立，则a的取值范围是（ ）
| 1 |
| 2 |
A、0＜a≤
| ||
B、0＜a＜
| ||
C、
| ||
D、
|
两条异面直线指的是（ ）
| A、没有公共点的两条直线 |
| B、分别位于两个不同平面的两条直线 |
| C、某一平面内的一条直线和这个平面外的一条直线 |
| D、不同在任何一个平面内的两条直线 |
下列一定在一个平面内的图形是（ ）
| A、垂直于同一直线的两条直线 |
| B、顺次首尾相连的四条线段 |
| C、两两相交的三条直线 |
| D、分别在两条异面直线上两点连线的中点的轨迹 |
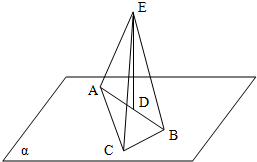如图，已知Rt△ABC在平面α内，D是斜边AB的中点，DE⊥α，且DE=12cm，AC=8cm，BC=6cm，求EA、EB、EC的长．