题目内容
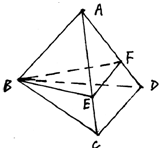 已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:
已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:(1)周长的最小值;
(2)周长最小时的截面面积.
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:(1)把正三棱锥A-BCD的侧面展开,两点间的连接线BB'即是截面周长的最小值.
(2)将该正三棱锥A-BCD沿AB边展开,得五边形ABCDB′,则AB=AC=AD=AB′=2a,BC=BD=DB′=a,直线BB′与AC、AD相交于E、F两点即为所求的最小周长时的两个点,由此能求出周长最小时的截面面积.
(2)将该正三棱锥A-BCD沿AB边展开,得五边形ABCDB′,则AB=AC=AD=AB′=2a,BC=BD=DB′=a,直线BB′与AC、AD相交于E、F两点即为所求的最小周长时的两个点,由此能求出周长最小时的截面面积.
解答:
解:(1)把正三棱锥A-BCD的侧面展开,两点间的连接线BB'即是截面周长的最小值.
∵BB′∥CD,∴△ADB′∽△B′FD,∴
=
,
∵AD=2a,DB''=a.∴DF=
,
又△AEF∽△ACD,∴
=
,其中CD=a,AD=2a,AF=2a-
=
,
∴EF=
,
∴截面周长最小值是BB′=2a+
a=
.
(2)将该正三棱锥A-BCD沿AB边展开
得五边形ABCDB′,则AB=AC=AD=AB′=2a,BC=BD=DB′=a
直线BB′与AC、AD相交于E、F两点即为所求的最小周长时的两个点
∵AB=AC=AD=AB′=2a,
∴BCDB′在以A为圆心2a为半径的圆上,
设角CAD=x,则sin(
)=
,cos(
)=
,
sinx=2×
×
=
,cosx=
,
则sin2x=2×
×
=
,cos2x=
,
sin(2x-
)=sin2xcos
-cos2xsin
=
×
-
×
=
,cos(
)=
,
EF=2tan(
)[2acos(
)]=2×
×
=
,
则BE=B′F=2asin(
)-
=2a×
-
=a,
所求的三角形三边分别为a,a,
,
cos∠EBF=
=
,sin∠EBF=
,
∴S△BEF=2a2×
=
.
∵BB′∥CD,∴△ADB′∽△B′FD,∴
| DF |
| DB′ |
| DB′ |
| AD |
∵AD=2a,DB''=a.∴DF=
| a |
| 2 |
又△AEF∽△ACD,∴
| EF |
| CD |
| AF |
| AD |
| a |
| 2 |
| 3a |
| 2 |
∴EF=
| 3a |
| 4 |
∴截面周长最小值是BB′=2a+
| 3 |
| 4 |
| 11a |
| 4 |
(2)将该正三棱锥A-BCD沿AB边展开
得五边形ABCDB′,则AB=AC=AD=AB′=2a,BC=BD=DB′=a
直线BB′与AC、AD相交于E、F两点即为所求的最小周长时的两个点
∵AB=AC=AD=AB′=2a,
∴BCDB′在以A为圆心2a为半径的圆上,
设角CAD=x,则sin(
| x |
| 2 |
| 1 |
| 4 |
| x |
| 2 |
| ||
| 4 |
sinx=2×
| 1 |
| 4 |
| ||
| 4 |
| ||
| 8 |
| 7 |
| 8 |
则sin2x=2×
| ||
| 8 |
| 7 |
| 8 |
7
| ||
| 32 |
| 17 |
| 32 |
sin(2x-
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
=
7
| ||
| 32 |
| ||
| 4 |
| 17 |
| 32 |
| 1 |
| 4 |
| 11 |
| 16 |
| 3x |
| 2 |
3
| ||
| 16 |
EF=2tan(
| x |
| 2 |
| 3x |
| 2 |
| 1 | ||
|
3a
| ||
| 8 |
| 3a |
| 4 |
则BE=B′F=2asin(
| 3x |
| 2 |
| EF |
| 2 |
| 11 |
| 16 |
| 3a |
| 8 |
所求的三角形三边分别为a,a,
| 3a |
| 4 |
cos∠EBF=
2a2-(
| ||
| 2a2 |
| 23 |
| 32 |
| ||
| 8 |
∴S△BEF=2a2×
| ||
| 8 |
| ||
| 4 |
点评:本题考查三角形周长的最小值的求法,考查周长最小时的截面面积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
下列推理是归纳推理的是( )
| A、A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆 | ||||
| B、科学家利用鱼的沉浮原理制造潜艇 | ||||
C、由圆x2+y2=r2的面积πr2,猜出椭圆
| ||||
| D、由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
两条异面直线指的是( )
| A、没有公共点的两条直线 |
| B、分别位于两个不同平面的两条直线 |
| C、某一平面内的一条直线和这个平面外的一条直线 |
| D、不同在任何一个平面内的两条直线 |
下列一定在一个平面内的图形是( )
| A、垂直于同一直线的两条直线 |
| B、顺次首尾相连的四条线段 |
| C、两两相交的三条直线 |
| D、分别在两条异面直线上两点连线的中点的轨迹 |
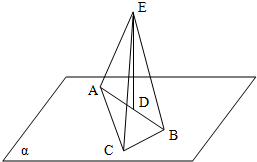 如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.
如图,已知Rt△ABC在平面α内,D是斜边AB的中点,DE⊥α,且DE=12cm,AC=8cm,BC=6cm,求EA、EB、EC的长.