题目内容
设等比数列{an}的前n项和为Sn,若a4,a3,a5成等差数列,且Sk=33,Sk+1=-63,其中k∈N*,则Sk+2的值为 .
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:根据a4,a3,a5成等差数列,求出公比q,代入Sk=33,Sk+1=-63,求出qk-1代入Sk+2即可求出结果.
解答:
解:设数列{an}的首项为a1,公比为q,
由已知得2a3=a4+a5,∴2a1q2=a1q3+a1q4
∵a1≠0,q≠0,∴q2+q-2=0,
解得q=1或q=-2,
当q=1时,与Sk=33,Sk+1=-63矛盾,故舍去,
∴q=-2,
∴Sk=
=33,Sk+1=
-63,解之得qk=-32,a1=3,
∴Sk+2=
=129,
故答案为:129.
由已知得2a3=a4+a5,∴2a1q2=a1q3+a1q4
∵a1≠0,q≠0,∴q2+q-2=0,
解得q=1或q=-2,
当q=1时,与Sk=33,Sk+1=-63矛盾,故舍去,
∴q=-2,
∴Sk=
| a1(1-qk) |
| 1-q |
| a1(1-qk) |
| 1-q |
∴Sk+2=
| 3[1-(-32)×4] |
| 1-(-2) |
故答案为:129.
点评:本题主要考查等比数列的性质,解本题的关键是运用等差数列的重要性质an-1+an+1=2an,要准确把握等差数列和等比数列的性质.属于中档题.

练习册系列答案
相关题目
| 2 |
| 1-i |
| A、1-i | B、1+i |
| C、2-i | D、2+i |
一个四棱锥的三视图如图所示,则此四棱至的四个侧面中的最大面积是( )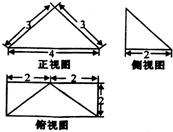

| A、3 | ||
B、2
| ||
| C、6 | ||
| D、8 |
