题目内容
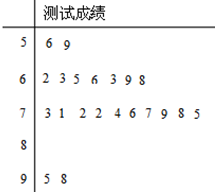 某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下:
某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下:| 分组 | 频数 | 频率 |
| [50,60﹚ | 0.08 | |
| [60,70﹚ | 7 | |
| [70,80﹚ | 10 | |
| [80,90﹚ | ||
| [90,100﹚ | 2 |
(Ⅰ)求班级的总人数;
(Ⅱ)将频率分布表补充完整;
(Ⅲ)若从[80,100﹚之间的数据中抽取2个进行分析,求至少有一个数据在[90,100﹚之间的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:计算题,概率与统计
分析:(I)根据茎叶图可得成绩在[50,60)之间的频数,由频率分布表可得频率,利用样本容量=
求得班级总人数;
(II)求得在[80,90)之间的频数,分别求得各组的频率,画频率分布表;
(III)根据成绩在[80,100)之间的数据共有6个,计算从中任取2个的取法种数和其中至少有一个数据在[90,100﹚之间的取法种数,代入古典概型概率公式计算.
| 频数 |
| 频率 |
(II)求得在[80,90)之间的频数,分别求得各组的频率,画频率分布表;
(III)根据成绩在[80,100)之间的数据共有6个,计算从中任取2个的取法种数和其中至少有一个数据在[90,100﹚之间的取法种数,代入古典概型概率公式计算.
解答:
解:(I)由茎叶图知:成绩在[50,60)之间的频数为2,又频率为0.08,
∴样本容量n=
=25,
∴班级总人数为25(人);
(II)在[80,90)之间的频数为25-2-7-10-2=4,
频率分布表如图:
(III)成绩在[80,100)之间的数据包括2组,在[80,90)之间的4个,在[90,100)之间的2个,
从中任取2个有
=15种取法,
其中至少有一个数据在[90,100﹚之间的取法有
+
×
=9种,
∴至少有一个数据在[90,100﹚之间的概率为
=
.
∴样本容量n=
| 2 |
| 0.08 |
∴班级总人数为25(人);
(II)在[80,90)之间的频数为25-2-7-10-2=4,
频率分布表如图:
| 分组 | 频数 | 频率 |
| [50,60﹚ | 2 | 0.08 |
| [60,70﹚ | 7 | 0.28 |
| [70,80﹚ | 10 | 0.40 |
| [80,90﹚ | 4 | 0.16 |
| [90,100﹚ | 2 | 0.08 |
从中任取2个有
| C | 2 6 |
其中至少有一个数据在[90,100﹚之间的取法有
| C | 2 2 |
| C | 1 2 |
| C | 1 4 |
∴至少有一个数据在[90,100﹚之间的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题考查了频率分布表与茎叶图的相关知识,考查了古典概型的概率计算,是概率统计的典型题目,解答本题要认真、细心.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=-x3-x+sinx,当θ∈(0,
)时,恒有f(cos2θ+2msinθ)+f(-2m-2)>0成立,则实数m的取值范围( )
| π |
| 2 |
A、(-∞,
| ||
B、(-∞,
| ||
C、(-
| ||
D、[-
|
一个四棱锥的三视图如图所示,则此四棱至的四个侧面中的最大面积是( )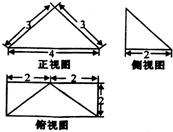

| A、3 | ||
B、2
| ||
| C、6 | ||
| D、8 |
