题目内容

若
C
0
n
+
C
1
n
2
+
C
2
n
3
+…+
C
n
n
n+1
=
31
n+1
，求n．
考点：组合及组合数公式
专题：计算题,排列组合
分析：由题意，
C
0
n
+
C
1
n
2
+
C
2
n
3
+…+
C
n
n
n+1
=
31
n+1
可化为
C
1
n+1
+
C
2
n+1
+
C
3
n+1
+…+
C
n+1
n+1
=31，从而利用二项展开式可得．
解答： 解：∵
C
0
n
+
C
1
n
2
+
C
2
n
3
+…+
C
n
n
n+1
=
31
n+1
，
∴（n+1）（
C
0
n
+
C
1
n
2
+
C
2
n
3
+…+
C
n
n
n+1
）=31，
∴
C
1
n+1
+
C
2
n+1
+
C
3
n+1
+…+
C
n+1
n+1
=31，
C
0
n+1
+
C
1
n+1
+
C
2
n+1
+
C
3
n+1
+…+
C
n+1
n+1
=31+1，
故2n+1=32，
即n+1=5，则n=4．
点评：本题考查了二项式定理的应用，属于基础题．
练习册系列答案
相关题目
已知直线l：2x-y+1=0与曲线C：y=mx2
（1）若只有一个交点，求实数m的值；
（2）若直线l与曲线C相交于A、B两点，且|AB|=2
10
，求实数m的值．
在各项均为正数的等比数列{an}中，若a2=1，a5=a3+2a1，则a3=
 
．
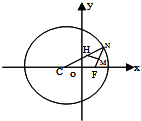已知点C为圆（x+1）2+y2=8的圆心，N是圆上的动点，点H在圆的半径CN上，且有点F（1，0）和FN上的点M，满足
MH
•
FN
=0，
FN
=2
FM
．
（Ⅰ）当点N在圆上运动时，求点H的轨迹E方程；
（Ⅱ）设曲线E与x轴正半轴、y轴正半轴的交点分别A，B，经过点(0，
2
)且斜率为k的直线l与曲线E有两个不同的交点P和Q，是否存在常数k，使得向量
OP
+
OQ
与
AB
共线？如果存在，求k值；如果不存在，请说明理由．
求下列数列{an}的通项公式：
（1）a1=
1
2
，an+1（1+an）=an；
（2）a1=1，（n+1）
a
2
n+1
-n
a
2
n
+an+1an=0；
（3）a1=1，（an，an+1）在直线y=2x+1上．
已知函数f（x）=loga（1+x），g（x）=loga（1-x），（a＞0，且a≠1）．
（1）设a=2，函数g（x）的定义域为[-63，-3]，求g（x）的最值；
（2）求使f（x）＞g（x）的x的取值范围．
已知函数f（x）的定义域R，当x＞0时，f（x）＞1，且对于任意的a，b∈R，恒有f（a+b）=f（a）×f（b），
（1）求f（0）的值；
（2）求证：当x＜0时，0＜f（x）＜1；
（3）求证：f（x）在区间（-∞，+∞）上是增函数．
已知f（x）=
3
sin（
π
8
x+
3
8
π），试求：
（1）函数的对称中心与对称轴方程；
（2）函数f（x）是由函数g（x）=cosx经过怎样的平移与伸缩变换得到的？
下列命题正确的个数是（　　）
①“在三角形ABC中，若sinA＞sinB，则A＞B”是真命题；
②函数 f（x）=cos2ax-sin2ax的最小正周期为“π是“a=1”的必要不充分条件；
③“?x∈R，x3-x2+1≤0”的否定是“?x∈R，x3-x2+1＞0”；
④向量
a
=（1，-2）与
b
=（1，m）的夹角为锐角，则m的取值范围为（-∞，
1
2
）．
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网