Question

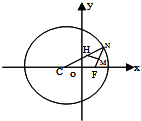已知点C为圆（x+1）²+y²=8的圆心，N是圆上的动点，点H在圆的半径CN上，且有点F（1，0）和FN上的点M，满足

MH

•

FN

=0，

FN

=2

FM

．
（Ⅰ）当点N在圆上运动时，求点H的轨迹E方程；
（Ⅱ）设曲线E与x轴正半轴、y轴正半轴的交点分别A，B，经过点(0，

2

)且斜率为k的直线l与曲线E有两个不同的交点P和Q，是否存在常数k，使得向量

OP

+

OQ

与

AB

共线？如果存在，求k值；如果不存在，请说明理由．

Answer 1

考点：直线与圆锥曲线的关系,轨迹方程

专题：计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程

分析：（Ⅰ）由题意知MH是线段FN的垂直平分线，运用垂直平分线的性质，可得|HC|+|HF|=|NC|=2

2

＞|CF|，再由椭圆的定义，即可得到轨迹E的方程；
（Ⅱ）由已知知直线的斜率必存在，设直线l的方程为：y=kx+

2

，联立椭圆方程，消去y，得到x的方程，由判别式大于0，运用韦达定理，运用向量的坐标和共线定理，即可得到斜率k，再加以检验即可判断．

解答： 解：（Ⅰ）由题意知MH是线段FN的垂直平分线，
于是|CN|=|HC|+|HN|=|HC|+|HF|=|NC|=2

2

＞|CF|，
所以点H的轨迹是以点C，F为焦点的椭圆，且a=

2

，c=1，所以b²=1，
故点的轨迹方程是：

x2

2

+y2=1；
（Ⅱ）由已知知直线的斜率必存在，设直线l的方程为：y=kx+

2

，
将其代入椭圆方程，整理得，（

1

2

+k²）x²+2

2

kx+1=0①
直线l与椭圆有两个不同的交点P，Q，所以△=8k²-4（

1

2

+k²）=4k²-2＞0，
解得k＞

2

2

或k＜-

2

2

②
设P（x₁，y₁），Q（x₂，y₂），则

OP

+

OQ

=（x₁+x₂，y₁+y₂），由①得，x₁+x₂=-

4 2 k

1+2k2

，
y₁+y₂=k（x₁+x₂）+2

2

，又A（

2

，0），B（0，1），

AB

=（-

2

，1），
所以

OP

+

OQ

与

AB

共线等价为

x1+x2=- 2 λ y1+y2=λ

，
即x₂+x₁=-

2

（y₁+y₂）=-

2

k（x₁+x₂）-4，
所以（1+

2

k）（x₁+x₂）=-4，
解得k=

2

2

不满足②，
所以满足条件的直线不存在．

点评：本题考查椭圆的定义、性质和方程，考查定义法求轨迹方程的方法，考查联立直线方程和椭圆方程，消去未知数，运用判别式大于0，韦达定理，平面向量的坐标运算和共线定理，考查运算能力，属于中档题．