题目内容
已知函数f(x)的定义域为[1,3],则函数f(2x-1)的定义域为( )
| A、[1,2] |
| B、[1,5] |
| C、[2,4] |
| D、[1,4] |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:由于函数f(x)的定义域为[1,3],则令2x-1∈[1,3],解得x,即得所求的定义域.
解答:
解:由于函数f(x)的定义域为[1,3],
则令2x-1∈[1,3],即有x∈[1,2],
则函数f(2x-1)的定义域为[1,2].
故选A.
则令2x-1∈[1,3],即有x∈[1,2],
则函数f(2x-1)的定义域为[1,2].
故选A.
点评:本题考查抽象函数定义域的求法,属中档题,注意理解函数f(x)的定义域与函数f[g(x)]定义域的区别.

练习册系列答案
相关题目
下列函数中,在其定义域内,既是奇函数又是减函数的是( )
A、f(x)=
| ||
B、f(x)=
| ||
| C、f(x)=-x3 | ||
| D、f(x)=2x-2-x |
下列各组函数中,表示同一函数的是( )
A、y=1,y=
| ||||||
B、y=
| ||||||
| C、y=2x+1-2x,y=2x | ||||||
| D、y=2lgx,y=lgx2 |
已知函数f(x)=
,若a>0,b>0,c>0,a+b>c,则( )
| x |
| x+1 |
| A、f(a)+f(b)>f(c) |
| B、f(a)+f(b)=f(c) |
| C、f(a)+f(b)<f(c) |
| D、以上结论都不对 |
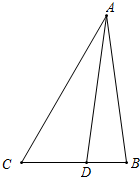 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2