题目内容
已知A(2,2),B(5,3),C(3,-1),求△ABC外接圆的方程.
考点:圆的标准方程
专题:直线与圆
分析:设圆的一般方程,利用待定系数法即可得到结论.
解答:
解:方程为x2+y2+Dx+Ey+F=0,将三点坐标代入,得
8+2D+2E+F=0,
34+5D+3E+F=0,
10+3D-E+F=0,
解得:D=-8,E=-2,F=12,
方程为x2+y2-8x-2y+12=0,
即(x-4)2+(y-1)2=5,
圆心为(4,1),半径为
.
8+2D+2E+F=0,
34+5D+3E+F=0,
10+3D-E+F=0,
解得:D=-8,E=-2,F=12,
方程为x2+y2-8x-2y+12=0,
即(x-4)2+(y-1)2=5,
圆心为(4,1),半径为
| 5 |
点评:本题主要考查圆的方程的求解,利用圆的方程的一般式,利用待定系数法是解决本题的关键.

练习册系列答案
相关题目
下列函数中,在其定义域内,既是奇函数又是减函数的是( )
A、f(x)=
| ||
B、f(x)=
| ||
| C、f(x)=-x3 | ||
| D、f(x)=2x-2-x |
已知函数f(x)=
,若a>0,b>0,c>0,a+b>c,则( )
| x |
| x+1 |
| A、f(a)+f(b)>f(c) |
| B、f(a)+f(b)=f(c) |
| C、f(a)+f(b)<f(c) |
| D、以上结论都不对 |
已知x>0时,(x-1)f′(x)<0,若△ABC是锐角三角形,则一定成立的是( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)>f(cosB) |
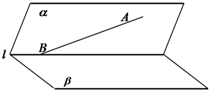 如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是
如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是