题目内容
为了解某班关注NBA是否与性别有关,对本班 48人进行了问卷调查得到如下的列联表:
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为
.
(1)请将上面列连表补充完整(不用写计算过程);
(2)判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
下列的临界值表,供参考
(参考公式:k2=
)其中 n=a+b+c+d.
| 关注NBA | 不关注NBA | 合 计 | |
| 男 生 | 6 | ||
| 女 生 | 10 | ||
| 合 计 | 48 |
| 2 |
| 3 |
(1)请将上面列连表补充完整(不用写计算过程);
(2)判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
下列的临界值表,供参考
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(1)利用所给数据可得列联表;
(20计算相关指数K2的观测值,比较临界值表,可得关注NBA与性别有关判断的可靠性程度
(20计算相关指数K2的观测值,比较临界值表,可得关注NBA与性别有关判断的可靠性程度
解答:
解:(1)列联表补充如下:
(2)由公式K2=
≈4.286,
∵4.286>3.841.
故有95%把握认为关注NBA与性别有关.
| 关注NBA | 不关注NBA | 合计 | |
| 男生 | 22 | 6 | 28 |
| 女生 | 10 | 10 | 20 |
| 合计 | 32 | 16 | 48 |
| 48×(22×10-10×6)2 |
| 28×20×32×16 |
∵4.286>3.841.
故有95%把握认为关注NBA与性别有关.
点评:本题考查独立性检验知识,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设集合M={x|0≤x≤2},N={y|0≤y≤2},给出下列4个图形,其中能表示集合M到N的函数关系的有( )
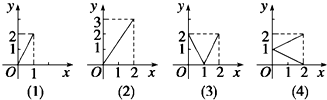

| A、0个 | B、1个 | C、2个 | D、3个 |
设圆C1:(x-1)2+y2=1与圆C2:(x-3)2+(y-2)2=1,点P为一动点,由点P作圆C1与圆C2的切线PA,PB,切点分别为A,B.若|PA|=|PB|,则点P的轨迹方程为( )
| A、x+y-3=0 |
| B、x+y+3=0 |
| C、x-y+3=0 |
| D、x-y-3=0 |
定义在(0,
)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
| π |
| 2 |
A、
| ||||||||
B、f(1)>2f(
| ||||||||
C、
| ||||||||
D、
|
已知f(
)=
,则f(x)=( )
| 1 |
| x |
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
| D、1+x |
等比数列{an}中,a1a3a5=8,则a3=( )
| A、1 | B、2 | C、3 | D、4 |