题目内容

设圆C1：（x-1）2+y2=1与圆C2：（x-3）2+（y-2）2=1，点P为一动点，由点P作圆C1与圆C2的切线PA，PB，切点分别为A，B．若|PA|=|PB|，则点P的轨迹方程为（　　）
A、x+y-3=0
B、x+y+3=0
C、x-y+3=0
D、x-y-3=0
考点：轨迹方程
专题：计算题,直线与圆
分析：利用|PA|=|PB|，结合勾股定理，即可求得点P的轨迹方程．
解答： 解：设P（x，y），则
∵|PA|=|PB|，
∴（x-1）2+y2-1=（x-3）2+（y-2）2-1，
∴x+y-3=0，
故选：A．
点评：本题考查点P的轨迹方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
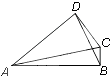如图，在四边形ABCD中，AB⊥BC，AD⊥DC．若
AB
=
a
，
AD
=
.
b
，则
AC
•
BD
=（　　）
A、
a
2-
b
2
B、
b
2-
a
2
C、
a
2+
b
2
D、
a
•
b
实数x，y满足
x≥0
x-2y≥0
2x-y-3≤0
．
（Ⅰ）求z=
y
x+1
的取值范围；
（Ⅱ）若函数z=ax+by（a＞0，b＞0）的最大值为3，求t=a•（1+b）的最大值．
执行如图所示的程序框图，如果输出s=3，那么判断框内应填入的条件是
 
．
已知函数f（x）=ax-
a
x
-2lnx．（a∈R）
（1）若a=2，求曲线f（x）在点（1，f（1））处的切线方程；
（2）若a＞0且函数f（x）在其定义域内为增函数，求实数a的取值范围；
（3）若函数y=f（x）在x∈（0，3）存在极值，求实数a的取值范围．
为了解某班关注NBA是否与性别有关，对本班 48人进行了问卷调查得到如下的列联表：
关注NBA不关注NBA合   计
男    生6
女    生10
合    计48
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为
2
3
．
（1）请将上面列连表补充完整（不用写计算过程）；
（2）判断是否有95%的把握认为关注NBA与性别有关？说明你的理由．
下列的临界值表，供参考
P（K2≥k0）0.100.050.0100.005
k02.7063.8416.6357.879
（参考公式：k2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
）其中 n=a+b+c+d．
已知函数f（x）=
1+x2
．
（Ⅰ） 设x1、x2都是实数，且x1≠x2，求证：|f（x2）-f（x1）|＜|x2-x1|；
（Ⅱ） 设a、b都是实数，且a2+b2=
1
2
，求证：f（a）+f（b）≤
5
．
某地为了调查职业满意度，决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中抽取若干人组成调查小组，相关数据见下表：
相关人员数抽取人数
公务员35b
教师a3
自由职业者284
则调查小组的总人数为（　　）
A、84B、12C、81D、14
设随机变量ξ服从正态分布N（2，9），若P（ξ＞a+b）=P（ξ＜a-b），则a=（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网