题目内容

等比数列{an}中，a1a3a5=8，则a3=（　　）
A、1B、2C、3D、4
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：根据等比数列的性质，得到a32=a1•a5，把已知条件代入即可求出a3的值．
解答： 解：由等比数列{an}中，a1a3a5=8，a32=a1•a5，得到a33=8，
解得：a3=2．
故选B．
点评：此题考查了等比数列的性质，利用a32=a1•a5是关键．
练习册系列答案
相关题目
为了解某班关注NBA是否与性别有关，对本班 48人进行了问卷调查得到如下的列联表：
关注NBA不关注NBA合   计
男    生6
女    生10
合    计48
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为
2
3
．
（1）请将上面列连表补充完整（不用写计算过程）；
（2）判断是否有95%的把握认为关注NBA与性别有关？说明你的理由．
下列的临界值表，供参考
P（K2≥k0）0.100.050.0100.005
k02.7063.8416.6357.879
（参考公式：k2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
）其中 n=a+b+c+d．
已知向量
m
=（sin2x，cosx），
n
=（
3
，2cosx）（x∈R），f（x）=
m
•
n
-1，
（1）求f（x）的单调递增区间．
（2）求f（x）在[0，
π
3
]的最大值和最小值．
已知关于x的不等式mx2-10x+2m2≤0的解集为A=[1，a]，集合B={x|log2（x2-x）＞1}．
（Ⅰ）求实数m，a的值；
（Ⅱ）求A∩B，（∁RA）∪B．
设随机变量ξ服从正态分布N（2，9），若P（ξ＞a+b）=P（ξ＜a-b），则a=（　　）
A、1B、2C、3D、4
下列计算正确的是（　　）
A、（-2a）2=2a2
B、a6÷a3=a2
C、-2（a-1）=2-2a
D、a•a2=a2
规定[t]为不超过t的最大整数，例如[12.6]=12，[-3.5]=-4，对任意实数x，令f1（x）=[4x]，g（x）=4x-[4x]，进一步令f2（x）=f1[g（x）]．
（1）若x=
7
16
，分别求f1（x）和f2（x）；
（2）若f1（x）=1，f2（x）=3同时满足，求x的取值范围．
下列函数中，满足“对任意x1，x2∈（0，+∞），当x1＜x2时，都有f（x1）＞f（x2）”的是（　　）
A、f（x）=（x-1）2
B、f（x）=
1
x
C、f（x）=ex
D、f（x）=lnx
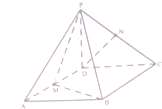已知四棱锥P-ABCD，底面ABCD是∠A=60°，边长为a的菱形，又PD⊥底面ABCD，且PD=CD，点M，N分别是棱AD，PC的中点．
（1）证明：DN∥平面PMB；
（2）证明：平面PMB⊥平面PAD；
（3）三棱锥A-PBM的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网