题目内容
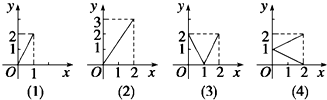
设集合M={x|0≤x≤2}，N={y|0≤y≤2}，给出下列4个图形，其中能表示集合M到N的函数关系的有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：函数的概念及其构成要素
专题：函数的性质及应用
分析：根据集合M到N的函数关系分别进行判断即可．
解答：
解：（1）．函数的定义域为[0，1]，而集合M={x|0≤x≤2}，∴（1）不能表示集合M到N的函数关系．
（2）．函数的定义域为[0，2]，值域为[0，3]，而N={y|0≤y≤2}，∴（2）不能表示集合M到N的函数关系．
（3）．函数的定义域为[0，2]，值域为[0，2]，而M={x|0≤x≤2}，N={y|0≤y≤2}，∴（3）满能表示集合M到N的函数关系
（4）．函数的定义域为[0，2]，值域为[0，2]，此时一个x有两个y值和x对应，∴（4）不能表示集合M到N的函数关系．
故选B．
（2）．函数的定义域为[0，2]，值域为[0，3]，而N={y|0≤y≤2}，∴（2）不能表示集合M到N的函数关系．
（3）．函数的定义域为[0，2]，值域为[0，2]，而M={x|0≤x≤2}，N={y|0≤y≤2}，∴（3）满能表示集合M到N的函数关系
（4）．函数的定义域为[0，2]，值域为[0，2]，此时一个x有两个y值和x对应，∴（4）不能表示集合M到N的函数关系．
故选B．
点评：本题主要考查函数的定义域，要求熟练掌握函数的定义，比较基础．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
用三种不同的颜色，将如图所示的4个区域涂色，每种颜色至少用1次，则相邻的区域不涂同一种颜色的概率为
实数x，y满足