题目内容
若-3＜a＜b＜2，则a-b的取值范围是 ．
考点：不等式的基本性质
专题：不等式的解法及应用
分析：由-3＜a＜b＜2，得出-3＜a＜2①，-2＜-b＜3②，a＜b③，综合①②③得出答案．
解答：
解：∵-3＜a＜b＜2，
∴-3＜a＜2①，-2＜-b＜3②，
①+②得：-5＜a+b＜5，
又a＜b，∴a-b＜0，
∴-5＜a-b＜0，
故答案为：（-5，0）．
∴-3＜a＜2①，-2＜-b＜3②，
①+②得：-5＜a+b＜5，
又a＜b，∴a-b＜0，
∴-5＜a-b＜0，
故答案为：（-5，0）．
点评：本题考查了不等式的性质问题，是一道基础题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知F1、F2分别是双曲线
-
=1（a＞0，b＞0）的左、右焦点，过点F1且斜率为k的直线与双曲线的右支交于点M，若点M在x轴上的射影恰好是右焦点F2，且
＜k＜
，则双曲线离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
| 4 |
| 3 |
| A、（1，2） |
| B、（1，3） |
| C、（3，+∞） |
| D、（2，3） |
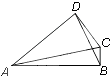如图，在四边形ABCD中，AB⊥BC，AD⊥DC．若| AB |
| a |
| AD |
. |
| b |
| AC |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
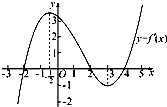如果函数y=f（x）的导函数的图象如图所示，给出下列判断：
用三种不同的颜色，将如图所示的4个区域涂色，每种颜色至少用1次，则相邻的区域不涂同一种颜色的概率为