题目内容
定义在(0,
)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
| π |
| 2 |
A、
| ||||||||
B、f(1)>2f(
| ||||||||
C、
| ||||||||
D、
|
考点:利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:把给出的等式变形得到f′(x)sinx-f(x)cosx>0,由此联想构造辅助函数g(x)=
,由其导函数的符号得到其在(0,
)上为增函数,对选项一一加以判断,即可得到答案.
| f(x) |
| sinx |
| π |
| 2 |
解答:
解:因为x∈(0,
),所以sinx>0,cosx>0.
由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx.
即f′(x)sinx-f(x)cosx>0.
令g(x)=
,x∈(0,
),则g′(x)=
>0.
所以函数g(x)=
在x∈(0,
)上为增函数,
对于A,由于g(
)<g(
),即
<
,化简即可判断A错;
对于B,由于g(1)>g(
),即
>
,化简即可判断B正确;
对于C,由于g(
)<g(
),即
<
,化简即可判断C错误;
对于D,由于g(
)<g(
),即
<
,所以
<
,
即
f(
)<f(
).故D错误.
故选B.
| π |
| 2 |
由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx.
即f′(x)sinx-f(x)cosx>0.
令g(x)=
| f(x) |
| sinx |
| π |
| 2 |
| f′(x)sinx-f(x)cosx |
| sin2x |
所以函数g(x)=
| f(x) |
| sinx |
| π |
| 2 |
对于A,由于g(
| π |
| 4 |
| π |
| 3 |
f(
| ||
sin
|
f(
| ||
sin
|
对于B,由于g(1)>g(
| π |
| 6 |
| f(1) |
| sin1 |
f(
| ||
sin
|
对于C,由于g(
| π |
| 6 |
| π |
| 4 |
f(
| ||
sin
|
f(
| ||
sin
|
对于D,由于g(
| π |
| 6 |
| π |
| 3 |
f(
| ||
sin
|
f(
| ||
sin
|
f(
| ||
|
f(
| ||||
|
即
| 3 |
| π |
| 6 |
| π |
| 3 |
故选B.
点评:本题考查了导数的运算法则,考查了利用函数导函数的符号判断函数的单调性,考查了函数构造法,属中档题型.

练习册系列答案
相关题目
21+
log25=( )
| 1 |
| 2 |
A、2+
| ||||
B、2
| ||||
C、2+
| ||||
D、1+
|
直线x-y+1=0截圆 x2+y2-2x-4y+1=0的弦长等于( )
| A、1 | B、2 | C、3 | D、4 |
下列计算正确的是( )
| A、(-2a)2=2a2 |
| B、a6÷a3=a2 |
| C、-2(a-1)=2-2a |
| D、a•a2=a2 |
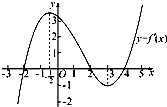 如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数的图象如图所示,给出下列判断: