题目内容
如直线l1、l2的斜率是二次方程x2-4x+1=0的两根,那么l1与l2的夹角是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两直线的夹角与到角问题
专题:
分析:设出两直线的斜率,由一元二次方程根与系数关系得到两直线斜率的和与积,代入夹角公式求得l1与l2的夹角.
解答:
解:设直线l1,l2的斜率分别为 k1,k2,l1与l2的夹角为θ,
则 k1+k2=4,k1•k2=1,
∴k1=2-
,k2=2+
.
则tanθ=|
|=|
|=
,
∴θ=
.
故选:A.
则 k1+k2=4,k1•k2=1,
∴k1=2-
| 3 |
| 3 |
则tanθ=|
| k2-k1 |
| 1+k1k2 |
2+
| ||||
1+(2-
|
| 3 |
∴θ=
| π |
| 3 |
故选:A.
点评:本题考查了两直线的夹角公式,考查了一元二次方程的根与系数关系,是基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
设圆柱的表面积为S,当圆柱体积最大时,圆柱的高为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、3π
|
点M是曲线
+
=1(x≠±5)上任意一点,点A,B的坐标分别为(-5,0),(5,0),直线AM与直线BM的斜率之积为( )
| x2 |
| 25 |
| y2 |
| 9 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为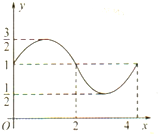 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
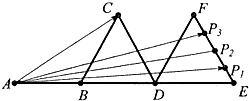 如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则
如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则