题目内容
已知抛物线y2=2px(p>0)上一点,A(1,
),F为抛物线的焦点,点A与F的连线交抛物线于另一点B,则BF= .
| 2 |
考点:抛物线的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:由点A(1,
)在抛物线y2=2px(p>0)上,可求出抛物线方程,进而求出F点的坐标,代入两点式,求出直线AB的方程,与抛物线方程联立后,可得B点的横坐标,再由抛物线的性质得到答案.
| 2 |
解答:
解:∵点A(1,
)在抛物线y2=2px(p>0)上,
故2=2p,解得p=1,
即抛物线方程为:y2=2x,其焦点为(
,0),
则直线AB的方程为:
=
,即y=2
x-
,
由
得:8x2-6x+2=0,
则B的横坐标x满足x+1=
,即x=
,
则B点到准线的距离d=
+
=
,
则BF=
,
故答案为:
| 2 |
故2=2p,解得p=1,
即抛物线方程为:y2=2x,其焦点为(
| 1 |
| 2 |
则直线AB的方程为:
x-
| ||
1-
|
| y | ||
|
| 2 |
| 2 |
由
|
则B的横坐标x满足x+1=
| 10 |
| 8 |
| 1 |
| 4 |
则B点到准线的距离d=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
则BF=
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题考查的知识点是抛物线的简单性质,直线方程,是直线与抛物线的综合应用,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为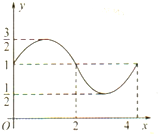 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
函数y=lnx+x的零点位于区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知异面直线l、m分别在平面α,β内,且α∩β=a,则直线a ( )
| A、同时与l、m都相交 |
| B、至少与l、m中的一条相交 |
| C、至多与l、m中的一条相交 |
| D、只能与l、m中的一条相交 |
函数y=
的最小正周期是( )
| 1-cos2x |
| sin2x |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
 在如图所示的平面图形中,已知
在如图所示的平面图形中,已知