题目内容
已知数列{an}的前n项和为Sn,且对于任意n∈N*都有Sn=2n-an.
(Ⅰ)计算a1,a2,a3,a4;
(Ⅱ)猜想该数列的通项公式an,并用数学归纳法证明猜想的正确性.
(Ⅰ)计算a1,a2,a3,a4;
(Ⅱ)猜想该数列的通项公式an,并用数学归纳法证明猜想的正确性.
考点:数学归纳法
专题:综合题,点列、递归数列与数学归纳法
分析:(Ⅰ)由题设条件,分别令n=1,2,3,4,能够求出a1,a2,a3,a4.
(Ⅱ)由(Ⅰ)猜想数列{an}的通项公式,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
(Ⅱ)由(Ⅰ)猜想数列{an}的通项公式,检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
解答:
解:(Ⅰ)因为Sn=2n-an,
所以a1=1,a2=
,a3=
,a4=
;
(Ⅱ)猜想an=
证明:①n=1时成立
②假设n=k时成立,即ak=
则n=k+1时,Sk+1=2(k+1)-ak+1,又Sk=2k-ak,
两式相减得:2ak+1=2+ak,
∴由假设及上式得:ak+1=
所以n=k+1时也成立
由①②知an=
,n∈N+时成立
所以a1=1,a2=
| 3 |
| 2 |
| 7 |
| 4 |
| 15 |
| 8 |
(Ⅱ)猜想an=
| 2n-1 |
| 2n-1 |
证明:①n=1时成立
②假设n=k时成立,即ak=
| 2k-1 |
| 2k-1 |
则n=k+1时,Sk+1=2(k+1)-ak+1,又Sk=2k-ak,
两式相减得:2ak+1=2+ak,
∴由假设及上式得:ak+1=
| 2k+1-1 |
| 2k |
所以n=k+1时也成立
由①②知an=
| 2n-1 |
| 2n-1 |
点评:本题是中档题,考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.注意在证明n=k+1时用上假设,化为n=k的形式.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设圆柱的表面积为S,当圆柱体积最大时,圆柱的高为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、3π
|
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为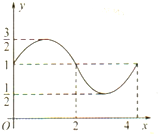 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
到两坐标轴距离相等的点的轨迹方程是( )
| A、y=x |
| B、x2-y2=0 |
| C、y=-x |
| D、y=|x| |
已知异面直线l、m分别在平面α,β内,且α∩β=a,则直线a ( )
| A、同时与l、m都相交 |
| B、至少与l、m中的一条相交 |
| C、至多与l、m中的一条相交 |
| D、只能与l、m中的一条相交 |
 如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.
如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.