题目内容
方程2x+3x-7=0在下列哪个区间有实根（ ）
| A、（-1，0） |
| B、（0，1） |
| C、（1，2） |
| D、（0，2） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：构造函数f（x）=2x+3x-7，可由根的存在性定理，结合答案代入验证两端点函数值异号即可．
解答：
解：令f（x）=2x+3x-7，
因为f（-1）=
-3-7＜0，
f（0）=1-7＜0，
f（1）=2+3-7=-2＜0，
f（2）=4+6-7=3＞0，
由根的存在性定理知方程2x+3x-7=0在（1，2）内有解．
故选C．
因为f（-1）=
| 1 |
| 2 |
f（0）=1-7＜0，
f（1）=2+3-7=-2＜0，
f（2）=4+6-7=3＞0，
由根的存在性定理知方程2x+3x-7=0在（1，2）内有解．
故选C．
点评：本题考查根的存在性定理，属基础知识的考查．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
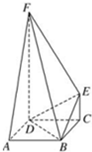如图，FD垂直于矩形ABCD所在平面，CE∥DF，∠DEF=90°．（1）求证：BE∥平面ADF；
（2）若矩形ABCD的一边AB=
| 3 |
| 3 |
| 3 |
已知|lga|=lgb（a＞0，b＞0），那么（ ）
| A、a=b | B、a=b或ab=1 |
| C、a=±b | D、ab=1 |
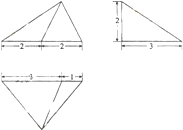若某几何体的三视图（单位：cm）如图所示（依次为正视图、侧视图、俯视图），则此几何体的体积是