题目内容
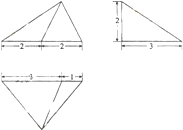 若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是
若某几何体的三视图(单位:cm)如图所示(依次为正视图、侧视图、俯视图),则此几何体的体积是考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据三视图判断几何体为一个以俯视图为底面的三棱锥,求出几何体的底面积和高,代入棱锥体积公式,可得答案.
解答:
解:根据三视图判断几何体为一个以俯视图为底面的三棱锥,
底面的底边长为4cm,高为3cm,
故底面面积S=
×4×3=6cm2,
棱锥的高h=2cm,
故棱锥的体积V=
Sh=4cm3,
故答案为:4
底面的底边长为4cm,高为3cm,
故底面面积S=
| 1 |
| 2 |
棱锥的高h=2cm,
故棱锥的体积V=
| 1 |
| 3 |
故答案为:4
点评:本题考查了由三视图求几何体的表面积与体积,根据三视图判断相关几何量的数据是解答问题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
方程2x+3x-7=0在下列哪个区间有实根( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(0,2) |
已知函数f(x)=sin2x向左平移
个单位后,得到函数y=g(x),下列关于y=g(x)的说法正确的是( )
| π |
| 6 |
A、一个対称中心为(-
| ||||
B、x=-
| ||||
C、减区间为[
| ||||
D、增区间为[kπ,
|
若向量
=(1,λ,2),
=(2,-1,2).
,
夹角的余弦值是
,则λ的值为( )
| a |
| b |
| a |
| b |
| 8 |
| 9 |
| A、2 | B、-2 | C、-3 | D、3 |
若a>0,b>0,且函数f(x)=4x3-ax2-2bx-2在x=1处有极值,则ab的最大值( )
| A、2 | B、3 | C、6 | D、9 |
已知a=2log52,b=21.1,c=(
)-0.8,则a、b、c的大小关系是( )
| 1 |
| 2 |
| A、.a<c<b |
| B、c<b<a |
| C、a<b<c |
| D、b<c<a |