题目内容
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加，则所选的3个人中至少有1个是非学生会干部的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：由组合数可得总的方法种数，间接法可得所选的3个人中至少有1个是非学生会干部的方法种数，由概率公式可得．
解答：
解：由题意从5人中选3人共有
=10种方法，
所选的3人全是学生会干部的有
=1种方法，
∴所选的3个人中至少有1个是非学生会干部共有10-1=9种方法，
∴所求事件的概率P=
故选：D
| C | 3 5 |
所选的3人全是学生会干部的有
| C | 3 3 |
∴所选的3个人中至少有1个是非学生会干部共有10-1=9种方法，
∴所求事件的概率P=
| 9 |
| 10 |
故选：D
点评：本题考查古典概型的概率公式，属基础题．
练习册系列答案
相关题目
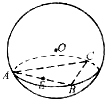已知正△ABC三个顶点都在半径为2的球面上，球心O到平面ABC的距离为1，点E是线段AB的中点，过点E作球O的截面，则截面面积的最小值是（ ）A、
| ||
| B、2π | ||
C、
| ||
| D、3π |
函数y=（2a2-3a+2）ax是指数函数，则a的取值范围是（ ）
| A、a＞0，a≠1 | ||
| B、0＜a＜1 | ||
C、a=
| ||
D、
|