题目内容
已知O为△ABC的外心,∠BAC=45°,若
•
=1,若
•
=2,则△ABC的面积为 .
| AO |
| AB |
| AO |
| AC |
考点:平面向量数量积的运算,余弦定理
专题:平面向量及应用
分析:先设AB=c,AC=b,外接圆的半径为R,利用余弦定理求出cos∠BAO、cos∠CAO,由条件和数量积运算求出边c、b,代入三角形的面积公式求出△ABC的面积.
解答:
解:设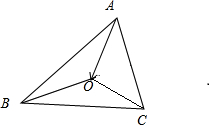 AB=c,AC=b,外接圆的半径为R,
AB=c,AC=b,外接圆的半径为R,
在△ABO中,由余弦定理得cos∠BAO=
=
=
,
同理可得,cos∠CAO=
,
因为
•
=1,
•
=2,
所以cR•
=1,bR•
=2,解得c=
,b=2,
又∠BAC=45°,
则△ABC的面积为S=
×|AB|×|AC|sin∠BAC=
×
×2×
=1,
故答案为:1.
 AB=c,AC=b,外接圆的半径为R,
AB=c,AC=b,外接圆的半径为R,在△ABO中,由余弦定理得cos∠BAO=
| AB2+AO2-BO2 |
| 2•AB•AO |
=
| c2+R2-R2 |
| 2cR |
| c |
| 2R |
同理可得,cos∠CAO=
| b |
| 2R |
因为
| AO |
| AB |
| AO |
| AC |
所以cR•
| c |
| 2R |
| b |
| 2R |
| 2 |
又∠BAC=45°,
则△ABC的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
故答案为:1.
点评:本题考查了平面向量数量积运算,余弦定理,三角形的面积公式,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在△ABC中,角A,B,C的对边分别为a,b,c,且b2+a2=c2+
ab,则内角C=( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列结论中正确的是( )
| A、偶函数的图象一定与y轴相交 |
| B、奇函数y=f(x)在x=0处有定义,则f(0)=0 |
| C、奇函数y=f(x)图象一定过原点 |
| D、图象过原点的奇函数必是单调函数 |
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加,则所选的3个人中至少有1个是非学生会干部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).