题目内容
设Sn为数列{an}的前n项和,对任意的n∈N*,都有Sn=(m+1)-man(m为正常数)
(1)求证:数列{an}是等比数列;
(2)数列{bn}满足:b1=2a1,bn=
(n≥2,n∈N+),求数列{bn}的通项公式;
(3)在满足(2)的条件下,求数列{
}的前n项和Tn.
(1)求证:数列{an}是等比数列;
(2)数列{bn}满足:b1=2a1,bn=
| bn-1 |
| 1+bn-1 |
(3)在满足(2)的条件下,求数列{
| 2n+1 |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知得a1=1,(1+m)an=man-1,从而
=
,(n≥2),由此能证明数列{an}是首项为1,公比为
的等比数列.
(2)由b1=2a1=2,bn=
(n≥2,n∈N+),得
-
=1,(n≥2),从而{
}是首项为
,公差为1的等差数列,由此能求出bn=
,(n∈N*).
(3)由bn=
,得
=2n(2n-1),由此利用错位相减法能求出数列{
}的前n项和Tn.
| an |
| an-1 |
| m |
| 1+m |
| m |
| 1+m |
(2)由b1=2a1=2,bn=
| bn-1 |
| 1+bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
| 1 |
| 2 |
| 2 |
| 2n-1 |
(3)由bn=
| 2 |
| 2n-1 |
| 2n+1 |
| bn |
| 2n+1 |
| bn |
解答:
(1)证明:当n=1时,a1=S1=(m+1)-ma1,解得a1=1,
当n≥2时,an=Sn-Sn-1=man-1-man,即(1+m)an=man-1,
∵m为常数,且m>0,∴
=
,(n≥2),
∴数列{an}是首项为1,公比为
的等比数列.
(2)解:由(1)得,b1=2a1=2,bn=
(n≥2,n∈N+),
∴
=
+1,即
-
=1,(n≥2),
∴{
}是首项为
,公差为1的等差数列,
∴
=
+(n-1)•1=
,
∴bn=
,(n∈N*).
(3)解:由(2)知,bn=
,则
=2n(2n-1),
∴Tn=2×1+22×3+23×5+…+2n×(2n-1),①
则2Tn=22×1+23×3+24×5+…+2n+1×(2n-1),②
②-①得,Tn=2n+1×(2n-1)-2-23-24-…-2n+1,
故Tn=2n+1×(2n-1)-2-
=2n+1×(2n-3)+6.
当n≥2时,an=Sn-Sn-1=man-1-man,即(1+m)an=man-1,
∵m为常数,且m>0,∴
| an |
| an-1 |
| m |
| 1+m |
∴数列{an}是首项为1,公比为
| m |
| 1+m |
(2)解:由(1)得,b1=2a1=2,bn=
| bn-1 |
| 1+bn-1 |
∴
| 1 |
| bn |
| 1 |
| bn-1 |
| 1 |
| bn |
| 1 |
| bn-1 |
∴{
| 1 |
| bn |
| 1 |
| 2 |
∴
| 1 |
| bn |
| 1 |
| 2 |
| 2n-2 |
| 2 |
∴bn=
| 2 |
| 2n-1 |
(3)解:由(2)知,bn=
| 2 |
| 2n-1 |
| 2n+1 |
| bn |
∴Tn=2×1+22×3+23×5+…+2n×(2n-1),①
则2Tn=22×1+23×3+24×5+…+2n+1×(2n-1),②
②-①得,Tn=2n+1×(2n-1)-2-23-24-…-2n+1,
故Tn=2n+1×(2n-1)-2-
| 23(1-2n-1) |
| 1-2 |
点评:本题考查等比数列的证明,考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加,则所选的3个人中至少有1个是非学生会干部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读如图所示的程序图,运行相应的程序输出的结果s=( )


| A、1 | B、4 | C、9 | D、16 |
设数列{an}是等差数列,公差d>0,Sn为其前n项和,若正整数i,j,k,l满足i<k<l<j,且i+j=k+l,则( )
| A、Si+Sj<Sk+Sl |
| B、Si+Sj>Sk+Sl |
| C、SiSj<SkSl |
| D、SiSj>SkSl |
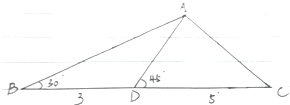 在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.
在△ABC中,BD=3,DC=5,∠B=30°,∠ADC═45° 求AC.