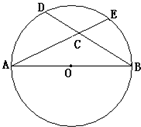
题目内容
已知双曲线C:
-
=1(a>0,b>0)的焦距为2c,焦点到双曲线C的渐近线的距离为
,则双曲线C的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,双曲线焦点到渐近线的距离为b=
,又b2=c2-a2,代入得4a2=3c2,即可求得双曲线C的离心率.
| c |
| 2 |
解答:
解:由题意,双曲线焦点到渐近线的距离为b=
,
又b2=c2-a2,代入得4a2=3c2,解得e=
,
故答案为:
.
| c |
| 2 |
又b2=c2-a2,代入得4a2=3c2,解得e=
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查双曲线的简单性质,考查双曲线中几何量之间的关系,考查数形结合的能力,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
设集合M={x|x=
+
,k∈Z},N={x|x=
+
,k∈Z},则( )
| k |
| 2 |
| 1 |
| 2 |
| k |
| 4 |
| 1 |
| 2 |
| A、M=N | B、M?N |
| C、M?N | D、M∩N=∅ |
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加,则所选的3个人中至少有1个是非学生会干部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=x(2-x).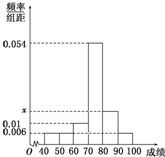 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: