题目内容
求函数f(x)=tan2x+2atanx+5在x∈[
,
]时的值域.
| π |
| 4 |
| π |
| 2 |
考点:复合三角函数的单调性
专题:函数的性质及应用,三角函数的求值
分析:首先通过恒等变换,把函数变形成标准的二次函数,进一步对参数a的范围和函数的定义域比较来进行分类讨论,最后求出结果.
解答:
解:函数f(x)=tan2x+2atanx+5=(tanx+a)2-a2+5
所以函数为以-a为对称轴,开口方向向上的抛物线.
由于x∈[
,
]
所以:tanx∈[1,+∞)
①当-a≤1时,即a≥-1在tanx=1处取得最小值,
所以函数的最小值为:ymin=6+2a
②当-a>1时,即a<-1在tanx=-a处取得最小值,
所以函数的最小值为:ymin=5-a2
综上所述①当a≥-1在tanx=1处取得最小值,函数的值域为:y∈[6+2a,+∞)
②当a<-1在tanx=-a处取得最小值,函数的值域为:y∈[5-a2,+∞)
所以函数为以-a为对称轴,开口方向向上的抛物线.
由于x∈[
| π |
| 4 |
| π |
| 2 |
所以:tanx∈[1,+∞)
①当-a≤1时,即a≥-1在tanx=1处取得最小值,
所以函数的最小值为:ymin=6+2a
②当-a>1时,即a<-1在tanx=-a处取得最小值,
所以函数的最小值为:ymin=5-a2
综上所述①当a≥-1在tanx=1处取得最小值,函数的值域为:y∈[6+2a,+∞)
②当a<-1在tanx=-a处取得最小值,函数的值域为:y∈[5-a2,+∞)
点评:本题考查的知识要点:复合函数的值域问题的应用,分类讨论思想的应用,属于基础题型.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
某项公益活动需要从3名学生会干部和2名非学生会干部中选出3人参加,则所选的3个人中至少有1个是非学生会干部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
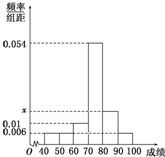 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: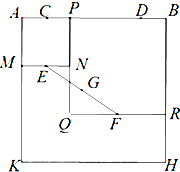 如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为
如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为