题目内容
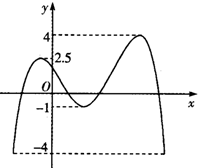
函数f(x)的图象如图所示,若函数y=2f(x-1)-c与x轴有四个不同交点,则c的取值范围是( )

| A、(-1,2.5) |
| B、(-1,5) |
| C、(-2,2.5) |
| D、(-2,5) |
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:函数y=2f(x-1)-c与x轴有四个不同交点,即方程2f(x-1)-c=0有四个不同的解,因此y=f(x-1)与y=
c有两个不同的交点,由图象即可得出.
| 1 |
| 2 |
解答:
解:函数y=2f(x-1)-c与x轴有四个不同交点,
即方程2f(x-1)-c=0有四个个不同的解,
由y=f(x-1)与y=
c有四个个不同的交点,
而函数f(x-1)是图象向右平移一个单位,不改变与x轴的交点的情况,
故y=f(x)与y=
c有四个个不同的交点,
由图象可知
c∈(-1,2.5).
故c∈(-2,5).
故选:D.
即方程2f(x-1)-c=0有四个个不同的解,
由y=f(x-1)与y=
| 1 |
| 2 |
而函数f(x-1)是图象向右平移一个单位,不改变与x轴的交点的情况,
故y=f(x)与y=
| 1 |
| 2 |
由图象可知
| 1 |
| 2 |
故c∈(-2,5).
故选:D.
点评:本题考查了函数的零点转化为函数图象交点的个数问题、数形结合思想方法,属于中档题.

练习册系列答案
相关题目
函数f(x)=
sin(
-
)的一个单调增区间为( )
| 3 |
| x |
| 2 |
| π |
| 4 |
A、(
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
A∉α,过A作与α平行的直线可作( )
| A、不存在 | B、一条 |
| C、四条 | D、无数条 |
cos37.5°sin97.5°-cos52.5°sin187.5°的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知函数f(x)=
x2-ax+(a-1)lnx(a>1),若对于任意x1,x2∈(0,+∞),x1≠x2,有
>-1,则实数a的取值范围为( )
| 1 |
| 2 |
| f(x 1)-f(x 2) |
| x1-x 2 |
| A、(1,4) |
| B、(1,4] |
| C、(1,5) |
| D、(1,5] |
在△ABC中,a,b,c分别是角A,B,C的对边,则与式子
相等的是( )
| b2+c2-a2 |
| 2bc |
| A、cosC | B、cosB |
| C、cosA | D、sinA |
已知定义在R上的函数y=f(x)对任意的x满足f(x+1)=-f(x),当-1≤x<1时,f(x)=x3.函数g(x)=
若函数h(x)=f(x)-g(x)在[-6,+∞)上有6个零点,则实数a的取值范围是( )
|
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、(
|