题目内容
在△ABC中，a，b，c分别是角A，B，C的对边，则与式子
相等的是（ ）
| b2+c2-a2 |
| 2bc |
| A、cosC | B、cosB |
| C、cosA | D、sinA |
考点：余弦定理
专题：解三角形
分析：利用余弦定理判断即可得到结果．
解答：
解：由余弦定理得：cosA=
，
故选：C．
| b2+c2-a2 |
| 2bc |
故选：C．
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
在△ABC中，若sin2A=sin2B+sin2C，则△ABC的形状是（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上答案均有可能 |
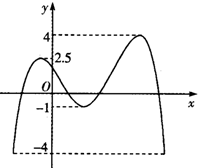
函数f（x）的图象如图所示，若函数y=2f（x-1）-c与x轴有四个不同交点，则c的取值范围是（ ）
| A、（-1，2.5） |
| B、（-1，5） |
| C、（-2，2.5） |
| D、（-2，5） |
已知f（x）=
，若对任意x∈[-1-a，a-1]，不等式f（
x-a）≥[f（x）]2恒成立，则实数a的取值范围是（ ）
|
| 2 |
A、（0，
| ||||
B、（0，
| ||||
C、（1，
| ||||
D、（1，
|
已知全集U=R，A={x|lgx≥0}，B={x|x＜x2}，则A∩（∁UB）=（ ）
| A、∅ | B、{1} |
| C、{0，1} | D、[0，1] |
已知
=（2，1），
=（x，1），且
+
与2
-
平行，则x等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、10 | B、-10 | C、2 | D、-2 |