题目内容
已知定义在R上的函数y=f(x)对任意的x满足f(x+1)=-f(x),当-1≤x<1时,f(x)=x3.函数g(x)=
若函数h(x)=f(x)-g(x)在[-6,+∞)上有6个零点,则实数a的取值范围是( )
|
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、(
|
考点:分段函数的应用,根的存在性及根的个数判断
专题:计算题,数形结合,函数的性质及应用
分析:f(x)=x3.函数g(x)=[-6,+∞)上有6个零点,即函数f(x)与g(x)的交点的个数,由函数图象的变换,分别做出y=f(x)与y=g(x)的图象,由此求得a的取值范围.
解答:
解:∵对任意的x满足f(x+1)=-f(x),∴f(x+2)=-f(x+1)=f(x),
即函数f(x)是以2为最小正周期的函数,画出函数f(x)、g(x)在[-6,+∞)的图象,
由图象可知:在y轴的左侧有2个交点,只要在左侧有4个交点即可.
则
即有
,故7<a≤9或
≤a<
.
故选:B.
即函数f(x)是以2为最小正周期的函数,画出函数f(x)、g(x)在[-6,+∞)的图象,

由图象可知:在y轴的左侧有2个交点,只要在左侧有4个交点即可.
则
|
|
| 1 |
| 9 |
| 1 |
| 7 |
故选:B.
点评:本题考查函数图象的变化与运用,涉及函数的周期性,对数函数的图象等知识点,关键是作出函数的图象,由此分析两个函数图象交点的个数.

练习册系列答案
相关题目
函数f(x)的图象如图所示,若函数y=2f(x-1)-c与x轴有四个不同交点,则c的取值范围是( )
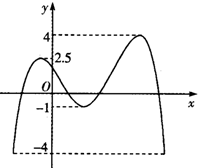

| A、(-1,2.5) |
| B、(-1,5) |
| C、(-2,2.5) |
| D、(-2,5) |
已知全集U=R,A={x|lgx≥0},B={x|x<x2},则A∩(∁UB)=( )
| A、∅ | B、{1} |
| C、{0,1} | D、[0,1] |
已知
=(2,1),
=(x,1),且
+
与2
-
平行,则x等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、10 | B、-10 | C、2 | D、-2 |
已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则
=( )
| b2 |
| a1+a2 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
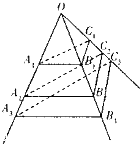 如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=
如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=