题目内容
求值:tan300°+sin420°= .
考点:运用诱导公式化简求值
专题:三角函数的图像与性质
分析:直接利用诱导公式化简求值即可.
解答:
解:tan300°+sin420°=tan(360°-60°)+sin(360°+60°)
=-tan60°+sin60°=-
+
=-
.
故答案为:-
=-tan60°+sin60°=-
| 3 |
| ||
| 2 |
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:本题考查诱导公式的应用,特殊角的三角函数值的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)的图象如图所示,若函数y=2f(x-1)-c与x轴有四个不同交点,则c的取值范围是( )
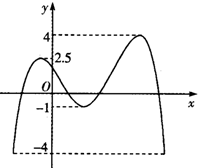

| A、(-1,2.5) |
| B、(-1,5) |
| C、(-2,2.5) |
| D、(-2,5) |
 已知半椭圆
已知半椭圆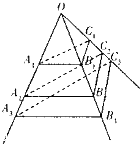 如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=
如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=