题目内容
函数f(x)=
sin(
-
)的一个单调增区间为( )
| 3 |
| x |
| 2 |
| π |
| 4 |
A、(
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
考点:复合三角函数的单调性
专题:三角函数的图像与性质
分析:由-
+2kπ≤
-
≤
+2kπ(k∈Z)可求得f(x)=
sin(
-
)的单调增区间为[-
+4kπ,
+2kπ](k∈Z),从而对k赋值,即可得到答案.
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
解答:
解:由-
+2kπ≤
-
≤
+2kπ(k∈Z)得:-
+4kπ≤x≤
+2kπ(k∈Z),
∴f(x)=
sin(
-
)的单调增区间为[-
+4kπ,
+2kπ](k∈Z),
令k=0得:f(x)=
sin(
-
)的一个单调增区间为(-
,
),
故选:C.
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
∴f(x)=
| 3 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
令k=0得:f(x)=
| 3 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
故选:C.
点评:本题考查复合三角函数的单调性,求得f(x)=
sin(
-
)的单调增区间为[-
+4kπ,
+2kπ](k∈Z)是关键,考查运算能力,属于中档题.
| 3 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
设x,y为正实数,且满足x≤2,y≤3,x+y=3,则4x3+y3的最大值是( )
| A、24 | B、27 | C、33 | D、45 |
若集合{1,a,
}={0,a2,a+b},则a2014+b2013的值为( )
| b |
| a |
| A、0 | B、1 | C、-1 | D、±1 |
在△ABC中,若sin2A=sin2B+sin2C,则△ABC的形状是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上答案均有可能 |
函数f(x)的图象如图所示,若函数y=2f(x-1)-c与x轴有四个不同交点,则c的取值范围是( )
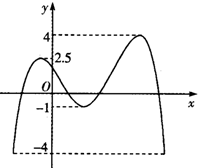

| A、(-1,2.5) |
| B、(-1,5) |
| C、(-2,2.5) |
| D、(-2,5) |
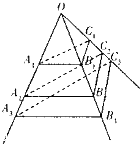 如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=
如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=