题目内容
A∉α,过A作与α平行的直线可作( )
| A、不存在 | B、一条 |
| C、四条 | D、无数条 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用直线与平面的位置关系求解.
解答:
解:∵A∉α,
∴过A作与α平行的直线可作出无数条.
故选:D.
∴过A作与α平行的直线可作出无数条.
故选:D.
点评:本题考查过平面外一点与平面平行的直线条数的判断,是基础题,解题时要注意空思维能力的培养.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
若集合{1,a,
}={0,a2,a+b},则a2014+b2013的值为( )
| b |
| a |
| A、0 | B、1 | C、-1 | D、±1 |
在△ABC中,若sin2A=sin2B+sin2C,则△ABC的形状是( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上答案均有可能 |
函数f(x)的图象如图所示,若函数y=2f(x-1)-c与x轴有四个不同交点,则c的取值范围是( )
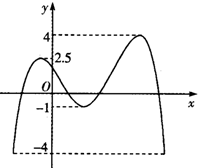

| A、(-1,2.5) |
| B、(-1,5) |
| C、(-2,2.5) |
| D、(-2,5) |
已知全集U=R,A={x|lgx≥0},B={x|x<x2},则A∩(∁UB)=( )
| A、∅ | B、{1} |
| C、{0,1} | D、[0,1] |
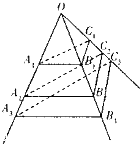 如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=
如图,互不相同的点A1,A2,…An,…,B1,B2,…,Bn,…C1,C2,…,Cn,…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn相互平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=