题目内容
已知函数f(x)=
x2-ax+(a-1)lnx(a>1),若对于任意x1,x2∈(0,+∞),x1≠x2,有
>-1,则实数a的取值范围为( )
| 1 |
| 2 |
| f(x 1)-f(x 2) |
| x1-x 2 |
| A、(1,4) |
| B、(1,4] |
| C、(1,5) |
| D、(1,5] |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求函数的导数,
>-1的几何意义为函数曲线上任意两点的割线斜率k>-1,转化为导数关系即可得到结论.
| f(x 1)-f(x 2) |
| x1-x 2 |
解答:
解:∵函数f(x)=
x2-ax+(a-1)lnx(a>1),
∴函数的导数f′(x)=x-a+
,
若对于任意x1,x2∈(0,+∞),x1≠x2,有
>-1,
即割线的斜率k>-1,
则等价为f′(x)=x-a+
≥-1恒成立,
即x+
≥a-1,
∵a>1,∴a-1>0,
则x+
≥2
=2
≥a-1,
即4(a-1)≥(a-1)2,即(a-1)(a-5)≤0,
解得1≤a≤5,
∵a>1,
∴1<a≤5,
故选:D
| 1 |
| 2 |
∴函数的导数f′(x)=x-a+
| a-1 |
| x |
若对于任意x1,x2∈(0,+∞),x1≠x2,有
| f(x 1)-f(x 2) |
| x1-x 2 |
即割线的斜率k>-1,
则等价为f′(x)=x-a+
| a-1 |
| x |
即x+
| a-1 |
| x |
∵a>1,∴a-1>0,
则x+
| a-1 |
| x |
x•
|
| a-1 |
即4(a-1)≥(a-1)2,即(a-1)(a-5)≤0,
解得1≤a≤5,
∵a>1,
∴1<a≤5,
故选:D
点评:本题主要考查导数的应用,根据函数单调性的几何意义以及斜率的关系,结合导数的几何意义是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
若集合{1,a,
}={0,a2,a+b},则a2014+b2013的值为( )
| b |
| a |
| A、0 | B、1 | C、-1 | D、±1 |
函数f(x)的图象如图所示,若函数y=2f(x-1)-c与x轴有四个不同交点,则c的取值范围是( )
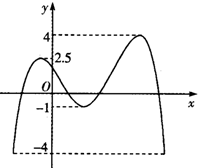

| A、(-1,2.5) |
| B、(-1,5) |
| C、(-2,2.5) |
| D、(-2,5) |
已知全集U=R,A={x|lgx≥0},B={x|x<x2},则A∩(∁UB)=( )
| A、∅ | B、{1} |
| C、{0,1} | D、[0,1] |
已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则
=( )
| b2 |
| a1+a2 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
 已知半椭圆
已知半椭圆 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=