题目内容
双曲线
-
=1(a>0,b>0)的一条渐近线方程y=
x,则离心率e= .
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由曲线
-
=1(a>0,b>0)的一条渐近线方程y=
x,推导出
=
,由此能求出双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| b |
| a |
| 3 |
解答:
解:∵双曲线
-
=1(a>0,b>0)的一条渐近线方程y=
x,
∴
=
,
∴e=
=
=
=
=2.
故答案为:2.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴
| b |
| a |
| 3 |
∴e=
| c |
| a |
| ||
| a |
=
1+(
|
=
1+(
|
=2.
故答案为:2.
点评:本题考查双曲线的离心率的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
7个人站一队,其中甲在排头,乙不在排尾,则不同的排列方法有( )
| A、720 | B、600 |
| C、576 | D、324 |
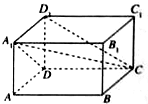 在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.
在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.