题目内容
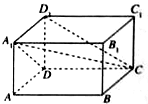 在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.
在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.考点:组合几何体的面积、体积问题
专题:计算题,空间位置关系与距离
分析:长方体看成直四棱柱ADD′A′-B′C′CB,设它的底面ADD′A′面积为S,高为h,求出棱锥C-A′DD′的体积,余下的几何体的体积,即可得到结果.
解答:
解:已知长方体是直四棱柱,
设它的底面ADD1A1的面积为S,高为h,…(2分)
则它的体积为V=Sh. …(4分)
而棱锥C-A1DD1的底面积为
S,高为h,…(6分)
故三棱锥C-A1DD1的体积:VC-A1DD1=
×
Sh=
Sh,…(8分)
余下部分体积为:Sh-
Sh=
Sh.…(10分)
∴棱锥C-A1DD1的体积与剩余部分的体积之比为1:5.…(12分)
设它的底面ADD1A1的面积为S,高为h,…(2分)
则它的体积为V=Sh. …(4分)
而棱锥C-A1DD1的底面积为
| 1 |
| 2 |
故三棱锥C-A1DD1的体积:VC-A1DD1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
余下部分体积为:Sh-
| 1 |
| 6 |
| 5 |
| 6 |
∴棱锥C-A1DD1的体积与剩余部分的体积之比为1:5.…(12分)
点评:本题是基础题,考查几何体的体积的有关计算,转化思想的应用,考查计算能力.

练习册系列答案
相关题目
设连续函数f(x)>0,则当a<b时,定积分
f(x)dx的符号( )
| ∫ | b a |
| A、一定是正的 |
| B、当0<a<b时为正,当a<b<0时为负 |
| C、一定是负的 |
| D、当0<a<b时为负,当a<b<0时为正 |
点P(x,y,z)满足(x-1)2+(y-1)2+(z+1)2=4,则点P在( )
| A、以点(1,1,-1)为圆心,以2为半径的圆上 |
| B、以点(1,1,-1)为中心,以2为棱长的正方体上 |
| C、以点(1,1,-1)为球心,以2为半径的球面上 |
| D、无法确定 |