题目内容
已知抛物线的顶点在原点,对称轴为x轴,焦点在双曲线
-
=1上,则抛物线方程为( )
| x2 |
| 4 |
| y2 |
| 2 |
| A、y2=8x |
| B、y2=4x |
| C、y2=2x |
| D、y2=±8x |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:抛物线的顶点在原点,对称轴为x轴,焦点在双曲线
-
=1上,故抛物线的顶点即为双曲线
-
=1的实轴顶点,结合双曲线的性质,和抛物线的性质可得答案.
| x2 |
| 4 |
| y2 |
| 2 |
| x2 |
| 4 |
| y2 |
| 2 |
解答:
解:∵抛物线的顶点在原点,对称轴为x轴,焦点在双曲线
-
=1上,
故抛物线的顶点即为双曲线
-
=1的实轴顶点,
由双曲线
-
=1的实轴顶点为(±2,0),
太抛物线方程为y2=±8x,
故选:D
| x2 |
| 4 |
| y2 |
| 2 |
故抛物线的顶点即为双曲线
| x2 |
| 4 |
| y2 |
| 2 |
由双曲线
| x2 |
| 4 |
| y2 |
| 2 |
太抛物线方程为y2=±8x,
故选:D
点评:本题考查的知识点是抛物线的简单性质,双曲线的简单性质,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
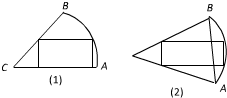 某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.
某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.