Question

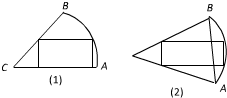某工厂生产主要产品后，留下大量中心角为60°，半径为a的扇形边角料，现要废物利用，从中剪裁出矩形毛坯，要求矩形面积尽可能大，并如图设计了两种裁剪方法，一种是使矩形的一边落在扇形的半径上，另一种是使矩形的两顶点分别在扇形的两条半径上，请选出最佳方案．

Answer 1

考点：已知三角函数模型的应用问题

专题：应用题,三角函数的求值

分析：分别求出面积，作差比较，即可得出结论．

解答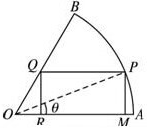： 解：方案一，如图，矩形有两个顶点在半径OA上，
 设∠AOP=θ，则PM=a•sinθ．
∵扇形中心角为60°，∴∠PQO=120°．
由正弦定理，得

OP

sin120°

=

PQ

sin(60°-θ)

，
∴PQ=

2

3

•a•sin（60°-θ）．
故矩形MPQR的面积为S₁=PM•PQ=

2

3

a²•sinθ•sin（60°-θ）
=

1

3

•a²[cos（2θ-60°）-cos60°]≤

1

3

•a²•（1-

1

2

）=

3

6

a²．
当cos（2θ-60°）=1．即θ=30°时，S₁取得最大值

3

6

a²．
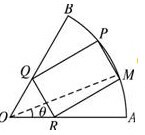
方案二：如图，矩形有两个顶点分别在扇形的两条半径OA、OB上．
设∠AOM=θ，∠MRA=

1

2

×60°=30°，∠MRO=150°，

由正弦定理，得

RM

sinθ

=

a

sin150°

．
∴RM=2a•sinθ．
又

OR

sin(30°-θ)

=

a

sin150°

．
∴OR=RQ=2a•sin（30°-θ）．
∴矩形MPQR的面积为
S₂=MR•RQ=4a²•sinθ•sin（30°-θ）
=2a²[cos（2θ-30°）-cos30°≤2a²•（1-

3

2

）=（2-

3

）a²，
即在此情况下，∠AOM=15°时，可求出M点，然后作出MPQR面积为最大．
由于S₁-S₂=

3

6

a²-（2-

3

）a²=

a2

6

（7

3

-12）＞0，
所以第一种方案能使截出的矩形面积最大，即∠AOP=θ=30°，使P取在AB弧中点，分别向扇形的一条半径作垂线及平行线得到矩形MPQR，即为最大矩形．

点评：本题考查正弦定理，考查学生利用数学知识解决实际问题的能力，属于中档题．