题目内容
图(1)是长方体截去一个角后得到的几何体,其中底面ABCD是正方形,H为AG中点,图(2)是该几何体的侧视图.
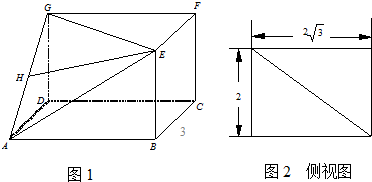
(Ⅰ)判断两直线EH与CD的位置关系,并给予证明;
(Ⅱ)求直线EH与平面BCFE所成角的大小.

(Ⅰ)判断两直线EH与CD的位置关系,并给予证明;
(Ⅱ)求直线EH与平面BCFE所成角的大小.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(Ⅰ)判断两直线EH与CD是相交直线,证明:说明H、D、C、E四点共面,HD∥CE,HD≠CE推出结果;
(Ⅱ)以D为原点,分别以DA、DC、DG为x、y、z轴,建立空间直角坐标系.求出平面BCFE的一个法向量是
=(0,2
,0),记直线EH与平面BCFE所成角为θ,利用向量的数量积即可求解直线EH与平面BCFE所成角的大小.
(Ⅱ)以D为原点,分别以DA、DC、DG为x、y、z轴,建立空间直角坐标系.求出平面BCFE的一个法向量是
| DC |
| 3 |
解答:
解:( I)直线EH和CD是相交直线.…(1分)
证明:连结HD,FB,CE,设FB与CE相交于点O,连结HO(如图1)
则四边形HDCO是平行四边形…(2分)
∴HD∥CO且HD=CO,∴HD∥CE且HD=
CE,
∴H、D、C、E四点共面…(4分)
又∵HD≠CE,
∴HE与CD必相交…(6分)
( II)由长方体的性质知,DA,DC,DG两两垂直,如图,以D为原点,分别以DA、DC、DG为x、y、z轴,建立空间直角坐标系.…(7分)
又由侧视图知:|BC|=2
,|CF|=2…(9分)
∴相关各点坐标为:D(0,0,0),A(2
,0,0),B(2
,2
,0),C(0,2
,0),E(2
,2
,2),F(0,2
,2),G(0,0,2),H(
,0,1),
∴
=(
,2
,1),…(10分)
又平面BCFE的一个法向量是
=(0,2
,0)
记直线EH与平面BCFE所成角为θ
∵
•
=
•0+2
•2
+1•0=12,|
|=4,|
|=2
,
∴sinθ=|
|=
=
…(12分)
又∵θ∈[0,
],∴θ=
…(13分)
∴直线EH与平面BCFE所成角为
.…(14分)
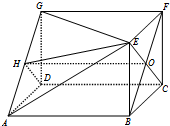

图1 图2
证明:连结HD,FB,CE,设FB与CE相交于点O,连结HO(如图1)
则四边形HDCO是平行四边形…(2分)
∴HD∥CO且HD=CO,∴HD∥CE且HD=
| 1 |
| 2 |
∴H、D、C、E四点共面…(4分)
又∵HD≠CE,
∴HE与CD必相交…(6分)
( II)由长方体的性质知,DA,DC,DG两两垂直,如图,以D为原点,分别以DA、DC、DG为x、y、z轴,建立空间直角坐标系.…(7分)
又由侧视图知:|BC|=2
| 3 |
∴相关各点坐标为:D(0,0,0),A(2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∴
| HE |
| 3 |
| 3 |
又平面BCFE的一个法向量是
| DC |
| 3 |
记直线EH与平面BCFE所成角为θ
∵
| HE |
| DC |
| 3 |
| 3 |
| 3 |
| HE |
| DC |
| 3 |
∴sinθ=|
| ||||
|
|
| 12 | ||
4•2
|
| ||
| 2 |
又∵θ∈[0,
| π |
| 2 |
| π |
| 3 |
∴直线EH与平面BCFE所成角为
| π |
| 3 |


图1 图2
点评:本题考查平面的基本性质的应用,直线与平面所成角的求法,向量法的应用,考查空间想象能力计算能力.

练习册系列答案
相关题目
已知抛物线的顶点在原点,对称轴为x轴,焦点在双曲线
-
=1上,则抛物线方程为( )
| x2 |
| 4 |
| y2 |
| 2 |
| A、y2=8x |
| B、y2=4x |
| C、y2=2x |
| D、y2=±8x |
函数f(x)=2x-x2的一个零点所在的区间为( )
| A、(-1,0) |
| B、(1,0) |
| C、(1,2) |
| D、(2,3) |