题目内容
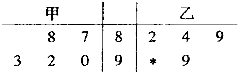 某校甲、乙两位学生在连续5次的月考中,成绩(均为整数)统计如茎叶图所示,其中一个数字被墨迹污染了,则甲的平均成绩不超过乙的平均成绩的概率是( )
某校甲、乙两位学生在连续5次的月考中,成绩(均为整数)统计如茎叶图所示,其中一个数字被墨迹污染了,则甲的平均成绩不超过乙的平均成绩的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:由已知的茎叶图,我们可以求出甲乙两人的平均成绩,然后求出<,即甲的平均成绩低于乙的平均成绩的概率,进而得到答案.
解答:
解:由已知中的茎叶图可得
甲的5次综合测评中的成绩分别为88,87,90,92,93,
则甲的平均成绩=
(88+87+90+92+93)=90
设污损数字为X,
则乙的5次综合测评中的成绩分别为82,84,89,99,90+X
则乙的平均成绩=(82+84+89+99+90+X)=88.8+
∵甲的平均成绩不超过乙的平均成绩
∴88.8+
≥90,
即X≥6,即为6,7,8,9一共4个数字
即甲的平均成绩低于乙的平均成绩的概率为
=
.
故选:B
甲的5次综合测评中的成绩分别为88,87,90,92,93,
则甲的平均成绩=
| 1 |
| 5 |
设污损数字为X,
则乙的5次综合测评中的成绩分别为82,84,89,99,90+X
则乙的平均成绩=(82+84+89+99+90+X)=88.8+
| X |
| 5 |
∵甲的平均成绩不超过乙的平均成绩
∴88.8+
| X |
| 5 |
即X≥6,即为6,7,8,9一共4个数字
即甲的平均成绩低于乙的平均成绩的概率为
| 4 |
| 10 |
| 2 |
| 5 |
故选:B
点评:本题考查的知识点是平均数,茎叶图,古典概型概率计算公式,其中根据已知茎叶图求出数据的平均数是解答本题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 如图,一个空间几何体的正视图与侧视图都是边长为1的正三角形,俯视图为正方形,则其体积是( )
如图,一个空间几何体的正视图与侧视图都是边长为1的正三角形,俯视图为正方形,则其体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a,b∈R,则下列命题正确的是( )
| A、若a>b,则a2>b2 |
| B、若|a|>b,则a2>b2 |
| C、若a>|b|,则a2>b2 |
| D、若a≠|b|,则a2≠b2 |
已知数列{an}满足a1+2a2+22a3+…+2n-1an=
,则an等于( )
| n |
| 2 |
| A、2n-1 | ||
B、(
| ||
C、(
| ||
| D、2n |
sin5°sin25°-sin95°sin65°的值是( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
甲、乙2人独立解答某道题,解答正确的概率分别为p1和p2,则甲、乙至少有1人解答正确的概率是( )
| A、p1+p2 |
| B、1-(1-p1)(1-p2) |
| C、1-p1p2 |
| D、p1p2 |
 一个几何体的三视图如图所示,则该几何体的体积是( )
一个几何体的三视图如图所示,则该几何体的体积是( )| A、π | B、2π | C、3π | D、4π |