题目内容
已知数列{an}满足a1+2a2+22a3+…+2n-1an=
,则an等于( )
| n |
| 2 |
| A、2n-1 | ||
B、(
| ||
C、(
| ||
| D、2n |
考点:数列递推式
专题:等差数列与等比数列
分析:由a1+2a2+22a3+…+2n-1an=
,得a2+2a2+22a3+…+2n-2an-1=
,由此能求出an.
| n |
| 2 |
| n-1 |
| 2 |
解答:
解:∵a1+2a2+22a3+…+2n-1an=
,①
a2+2a2+22a3+…+2n-2an-1=
,②
①-②,得:2n-1an=
,
an=
,(n>1).
a1=
也满足,
∴an=
.
故选:B.
| n |
| 2 |
a2+2a2+22a3+…+2n-2an-1=
| n-1 |
| 2 |
①-②,得:2n-1an=
| 1 |
| 2 |
an=
| 1 |
| 2n |
a1=
| 1 |
| 2 |
∴an=
| 1 |
| 2n |
故选:B.
点评:本题考查数列的通项公式的求法,解题时要认真审题,注意递推公式的合理运用.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )A、20+12
| ||
B、20+12
| ||
C、20+12
| ||
| D、32 |
cos110°cos50°+sin110°sin50°等于( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
| ∫ | 1 -1 |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
下列命题中,正确的是:( )
| A、若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行 |
| B、垂直于同一直线的两条直线相互平行 |
| C、若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 |
| D、平行于同一直线的两个平面互相平行 |
已知sin(
-α)=
,那么cos(
-α)=( )
| π |
| 6 |
| 1 |
| 2 |
| 2π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
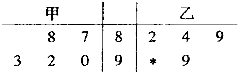 某校甲、乙两位学生在连续5次的月考中,成绩(均为整数)统计如茎叶图所示,其中一个数字被墨迹污染了,则甲的平均成绩不超过乙的平均成绩的概率是( )
某校甲、乙两位学生在连续5次的月考中,成绩(均为整数)统计如茎叶图所示,其中一个数字被墨迹污染了,则甲的平均成绩不超过乙的平均成绩的概率是( )