题目内容
 如图,一个空间几何体的正视图与侧视图都是边长为1的正三角形,俯视图为正方形,则其体积是( )
如图,一个空间几何体的正视图与侧视图都是边长为1的正三角形,俯视图为正方形,则其体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:易得此几何体为四棱锥,利用相应的三角函数可得四棱锥的高,体积=
×底面积×高,把相关数值代入即可求解.
| 1 |
| 3 |
解答:
解:由主视图和左视图为等腰三角形可得此几何体为锥体,由俯视图为四边形可得此几何体为四棱锥,
∵主视图为边长为1的正三角形,
∴正三角形的高,也就是棱锥的高为
,俯视图的边长为1,
∴四棱锥的体积=
×1×1×
=
,
故选C.
∵主视图为边长为1的正三角形,
∴正三角形的高,也就是棱锥的高为
| ||
| 2 |
∴四棱锥的体积=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
故选C.
点评:解决本题的关键是得到该几何体的形状,易错是确定四棱锥的底面边长与高的大小.

练习册系列答案
相关题目
已知a,b满足-1≤a+2b≤2,2≤2a-b≤3,则a+b的范围是( )
A、[-
| ||||
B、[-
| ||||
C、[0,
| ||||
D、[0,
|
下列判断正确的是( )
| A、命题“若x2=1,则x=1”的否命题是“若x2=1,则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、△ABC中,“A>B”是“cos2A<cos2B”的充要条件 |
| D、命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1<0” |
 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )A、20+12
| ||
B、20+12
| ||
C、20+12
| ||
| D、32 |
已知集合A={x|-1<x<1},B={x|x(x-2)<0},则A∩B( )
| A、{x|-1<x<0} |
| B、{x|0<x<1} |
| C、{x|-1<x<2} |
| D、{x|x>2} |
cos110°cos50°+sin110°sin50°等于( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
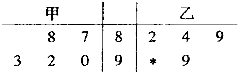 某校甲、乙两位学生在连续5次的月考中,成绩(均为整数)统计如茎叶图所示,其中一个数字被墨迹污染了,则甲的平均成绩不超过乙的平均成绩的概率是( )
某校甲、乙两位学生在连续5次的月考中,成绩(均为整数)统计如茎叶图所示,其中一个数字被墨迹污染了,则甲的平均成绩不超过乙的平均成绩的概率是( )