题目内容
已知tanα=2．求：
（1）
；
（2）4sin2α-3sinαcosα-5cos2α．
（1）
| 2sinα-3cosα |
| 4sinα-9cosα |
（2）4sin2α-3sinαcosα-5cos2α．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）将所求关系式的分子、分母同除cosα，将弦化切，再将tanα=2代入计算即可；
（2）将所求关系式转化为
，再将tanα=2代入计算即可．
（2）将所求关系式转化为
| 4tan2α-3tanα-5 |
| tan2α+1 |
解答：
解 （1）
=
=
=-1．
（2）4sin2α-3sin αcos α-5cos2α=
=
=
=1．
| 2sinα-3cosα |
| 4sinα-9cosα |
| 2tanα-3 |
| 4tanα-9 |
| 2×2-3 |
| 4×2-9 |
（2）4sin2α-3sin αcos α-5cos2α=
| 4sin2α-3sinαcosα-5cos2α |
| sin2α+cos2α |
=
| 4tan2α-3tanα-5 |
| tan2α+1 |
| 4×4-3×2-5 |
| 4+1 |
点评：本题考查同角三角函数基本关系的运用，考查转化思想与运算求解能力，属于中档题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
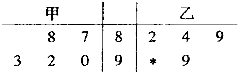某校甲、乙两位学生在连续5次的月考中，成绩（均为整数）统计如茎叶图所示，其中一个数字被墨迹污染了，则甲的平均成绩不超过乙的平均成绩的概率是（ ）
某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出1盒该产品获利润50元，未售出的产品，每盒亏损30元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了160盒该产品，以X（单位：盒，100≤X≤200）表示这个丌学季内的市场需求量，Y（单位：元）表示这个开学季内经销该产品的利润．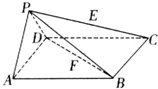
如图所示，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA=PD=