题目内容
已知a，b∈R，则下列命题正确的是（ ）
| A、若a＞b，则a2＞b2 |
| B、若|a|＞b，则a2＞b2 |
| C、若a＞|b|，则a2＞b2 |
| D、若a≠|b|，则a2≠b2 |
考点：不等关系与不等式
专题：不等式的解法及应用
分析：举反例可排除ABD，至于C由不等式的性质平方可证．
解答：
解：选项A，取a=-1，b=-2，显然满足a＞b，但不满足a2＞b2，故错误；
选项B，取a=-1，b=-2，显然满足|a|＞b，但不满足a2＞b2，故错误；
选项D，取a=-1，b=1，显然满足a≠|b|，但a2=b2，故错误；
选项C，由a＞|b|和不等式的性质，平方可得a2＞b2，故正确．
故选：C．
选项B，取a=-1，b=-2，显然满足|a|＞b，但不满足a2＞b2，故错误；
选项D，取a=-1，b=1，显然满足a≠|b|，但a2=b2，故错误；
选项C，由a＞|b|和不等式的性质，平方可得a2＞b2，故正确．
故选：C．
点评：本题考查不等式与不等关系，举反例是解决问题的关键，属基础题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
下列判断正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题是“若x2=1，则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、△ABC中，“A＞B”是“cos2A＜cos2B”的充要条件 |
| D、命题“?x∈R，使得x2+x+1＜0”的否定是“?x∈R，均有x2+x+1＜0” |
已知集合A={x|-1＜x＜1}，B={x|x（x-2）＜0}，则A∩B（ ）
| A、{x|-1＜x＜0} |
| B、{x|0＜x＜1} |
| C、{x|-1＜x＜2} |
| D、{x|x＞2} |
cos110°cos50°+sin110°sin50°等于（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
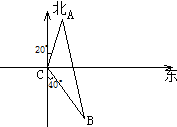如图，已知两座灯塔A和B与海洋观察站C的距离都等于1km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（ ）| A、1km | ||
B、
| ||
C、
| ||
| D、2km |
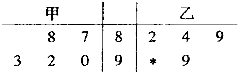某校甲、乙两位学生在连续5次的月考中，成绩（均为整数）统计如茎叶图所示，其中一个数字被墨迹污染了，则甲的平均成绩不超过乙的平均成绩的概率是（ ）某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、8 | ||
| D、4 |